搜索
【题目】计算：
（1）
﹣（ 
+ 
）÷ 
× 
（2）（ 
﹣4 
）﹣（3 
﹣2 
）
（3）（3+ ）（3﹣ ）﹣（ ﹣1）2
（4）（﹣ +1）（ ﹣1）﹣ 
+ 
．
参考答案：
【答案】
（1）解：原式= 
﹣（ 
+ 
）× 
× 
= ﹣（ + ）× 
= ﹣1﹣
=﹣1；
（2）解：原式=4 ﹣ ﹣ +
=3
（3）解：原式=9﹣5﹣（3﹣2 +1）
=4﹣4+2
=2 ；
（4）解：原式=﹣（3﹣2 +1）﹣3﹣（ +2）
=﹣4+2 ﹣3﹣ ﹣2
=2 ﹣ ﹣9
【解析】（1）先进行二次根式的乘除运算得到原式= ﹣（ + ）× ，然后进行二次根式的除法运算后合并即可；（2）先把各二次根式化简为最简二次根式，然后合并即可；（3）利用平方差公式和完全平方公式计算；（4）利用完全平方公式和分母有理化得到原式=﹣（3﹣2 +1）﹣3﹣（ +2），然后去括号后合并即可．
【考点精析】认真审题，首先需要了解二次根式的混合运算(二次根式的混合运算与实数中的运算顺序一样，先乘方，再乘除，最后加减，有括号的先算括号里的（或先去括号）)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，有点A（0，4）、B（9，4）、C（12，0）．已知点P从点A出发沿着AB路线向点B运动，点Q从点C出发沿CO路线向点O运动，运动速度都是每秒2个单位长度，运动时间为t秒．
（1）当t=4.5秒时，判断四边形AQCB的形状，并说明理由．
（2）当四边形AOQB是矩形时，求t的值．
（3）是否存在某一时刻，使四边形PQCB是菱形？若存在，求出t的值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】某学校活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：
操作发现：
（1）已知，△ABC，如图1，分别以AB和AC为边向△ABC外侧作等边△ABD和等边△ACE，连接BE、CD，请你完成作图 ， 并猜想BE与CD的数量关系是 ． （要求：尺规作图，不写作法但保留作图痕迹）
类比探究：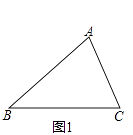
（2）如图2，分别以AB和AC为边向△ABC外侧作正方形ABDE和正方形ACFG，连接CE、BG，则线段CE、BG有什么关系？说明理由．
灵活运用：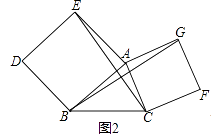
（3）如图3，已知△ABC中，∠ABC=45°，AB=2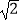
，BC=3，过点A作EA⊥AC，垂足为A，且满足AC=AE，求BE的长．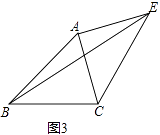
-
科目： 来源： 题型：
查看答案和解析>>【题目】今年，我国政府为减轻农民负担，决定在 5 年内免去农业税．某乡今年人均上缴农业税 25 元，若两年后人均上缴农业税为 16 元，假设这两年降低的百分率相同
（1）求降低的百分率；
（2）小红所在的乡约有 16000 农民，问该乡农民明年减少多少农业税？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果xm-3·xn＝x2，则n等于( )
A. m－1 B. 5－m C. 4－m D. m＋5
-
科目： 来源： 题型：
查看答案和解析>>【题目】一元二次方程x2﹣6x﹣5=0配方组可变形为（ ）
A.（x﹣3）2=14
B.（x﹣3）2=4
C.（x+3）2=14
D.（x+3）2=4 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，河的两岸
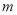与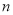
互相平行，A、B、C是
上的三点，P、Q是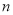
上的两点.在A处测得∠QAB=30°，在B处测得∠QBC=60°，在C处测得∠PCB=45°，已知AB=BC=20米，求PQ的长（结果保留根号）.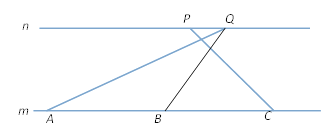
相关试题
