【题目】推理填空:
已知:如图,![]() ,
,![]() ,
,![]() .求
.求![]() 的度数.
的度数.

解:∵![]() ,
,
∴![]() .( )
.( )
又∵![]() ,
,
∴![]() .
.
∴![]() .( )
.( )
∴![]()
![]() ( ).
( ).
又∵![]() ,
,
∴![]() .
.
参考答案:
【答案】∠3,两直线平行,同位角相等;DG,内错角相等,两直线平行;∠AGD,两直线平行,同旁内角互补;110°,补角定义.
【解析】
由EF与AD平行,利用两直线平行,同位角相等得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到AB与DG平行,利用两直线平行同旁内角互补得出∠BAC+∠DGA=180°,即可得出结果.
解:∵EF∥AD,
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥DG(内错角相等,两直线平行)
∴∠BAC+∠AGD=180° (两直线平行,同旁内角互补)
又∵![]() ,
,
∴∠AGD=180°70°=110°(补角定义)
故答案为:∠3,两直线平行,同位角相等;DG,内错角相等,两直线平行;∠AGD,两直线平行,同旁内角互补;110°,补角定义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),AB⊥BD于点B,ED⊥BD于点D,点C是BD上一点.且BC=DE,CD=AB.

(1)试判断AC与CE的位置关系,并说明理由;
(2)如图(2),若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第(1)问中AC与BE的位置关系还成立吗?(注意字母的变化)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,先把一矩形
 纸片上下对折,设折痕为
纸片上下对折,设折痕为 ;如图②,再把
;如图②,再把点
 叠在折痕线
叠在折痕线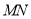 上,得到
上,得到
 .过
.过 点作
点作 ,分别交
,分别交 、
、 于点
于点 、
、 .
.(1)求证:
 ∽
∽ ;
;(2)在图②中,如果沿直线
 再次折叠纸片,点
再次折叠纸片,点 能否叠在直线
能否叠在直线 上?请说明理由;
上?请说明理由;(3)在(2)的条件下,若
 ,求
,求 的长度.
的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,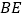 平分
平分 ,
, 平分
平分 ,
,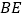 和
和 交于点
交于点 ,过点
,过点 作
作 交
交 于点
于点 ,交
,交 于点
于点 .若
.若 ,则
,则 的长为( )
的长为( )
A.6.5B.7.2C.8D.9.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
(1)经过几秒△PCQ的面积为△ACB的面积的
 ?
?(2)经过几秒,△PCQ与△ACB相似?
(3)如图2,设CD为△ACB的中线,那么在运动的过程中,PQ与CD有可能互相垂直吗?若有可能,求出运动的时间;若没有可能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一枚质地均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”, 3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这枚骰子掷出后:

(1)数字几朝上的概率最小?
(2)奇数面朝上的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列给出的条件中,能判定四边形ABCD为平行四边形的是()
A.AB=BC,CD=DAB.AB//CD,AD=BC
C.AB//CD,∠A=∠CD.∠A=∠B,∠C=∠D
相关试题

