【题目】如图①,先把一矩形![]() 纸片上下对折,设折痕为
纸片上下对折,设折痕为![]() ;如图②,再把
;如图②,再把
点![]() 叠在折痕线
叠在折痕线![]() 上,得到
上,得到![]()
![]() .过
.过![]() 点作
点作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(1)求证: ![]() ∽
∽![]() ;
;
(2)在图②中,如果沿直线![]() 再次折叠纸片,点
再次折叠纸片,点![]() 能否叠在直线
能否叠在直线![]() 上?请说明理由;
上?请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的长度.
的长度.

参考答案:
【答案】(1)(2)见解析;(3)![]()
【解析】试题分析:(1)由题意可以得到∠BPE=∠AQB=90°,通过角的转化可以得到∠BEP=∠ABQ,从而可以得到△PBE∽△QAB;
(2)根据折叠的知识可以得到QB=PB,由第(1)问中的相似可以得到对应边成比例,通过转化可以得到△PBE∽△BAE,从而可以解答本题;
(3)由题意和第(2)问可以得到∠AEB=∠BEP=60°,∠ABE=90°,又因为AB=![]() ,sin∠AEB=
,sin∠AEB=![]() ,从而可以得到AE的长度.
,从而可以得到AE的长度.
试题解析:(1)证明:∵PQ⊥MN,BN∥EC∥AD,∴∠BPE=∠AQB=∠PBN=∠NBQ=90°,∴∠PBE+∠BEP=90°,又∵∠PBE+∠ABQ=180°﹣∠ABE=180°﹣90°=90°,∴∠BEP=∠ABQ,在△PBE和△QAB中,∵∠BPE=∠AQB,∠BEP=∠ABQ,∴△PBE∽△QAB;
(2)点A能叠在直线EC上,理由:∵△PBE∽△QAB,∴ ![]() ,∵由折叠可知,QB=PB,∴
,∵由折叠可知,QB=PB,∴![]() ,即
,即![]() ,又∵∠ABE=∠BPE=90°,∴△PBE∽△BAE,∴∠AEB=∠PEB,∴沿直线EB再次折叠纸片,点A能叠在直线EC上;
,又∵∠ABE=∠BPE=90°,∴△PBE∽△BAE,∴∠AEB=∠PEB,∴沿直线EB再次折叠纸片,点A能叠在直线EC上;
(3)解:由(2)可知,∠AEB=∠PEB,而由折叠过程知:2∠AEB+∠PEB=180°,∴∠AEB=∠PEB=60°,在Rt△ABE中,sin∠AEB=![]() ,∴AE=
,∴AE= .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 (x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.
(x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.(1)求一次函数的解析式;
(2)根据图象直接写出不等式kx+b﹣
 >0的解集;
>0的解集;(3)求△AOB的面积;
(4)若点P在x轴上、点Q在y轴上,且以P、Q、A、B为顶点的四边形是平行四边形,请直接写出点P、Q的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),AB⊥BD于点B,ED⊥BD于点D,点C是BD上一点.且BC=DE,CD=AB.

(1)试判断AC与CE的位置关系,并说明理由;
(2)如图(2),若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第(1)问中AC与BE的位置关系还成立吗?(注意字母的变化)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,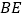 平分
平分 ,
, 平分
平分 ,
,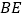 和
和 交于点
交于点 ,过点
,过点 作
作 交
交 于点
于点 ,交
,交 于点
于点 .若
.若 ,则
,则 的长为( )
的长为( )
A.6.5B.7.2C.8D.9.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
已知:如图,
 ,
, ,
, .求
.求 的度数.
的度数.
解:∵
 ,
,∴
 .( )
.( )又∵
 ,
,∴
 .
.∴
 .( )
.( )∴

 ( ).
( ).又∵
 ,
,∴
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
(1)经过几秒△PCQ的面积为△ACB的面积的
 ?
?(2)经过几秒,△PCQ与△ACB相似?
(3)如图2,设CD为△ACB的中线,那么在运动的过程中,PQ与CD有可能互相垂直吗?若有可能,求出运动的时间;若没有可能,请说明理由.

相关试题

