【题目】如图1,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
(1)经过几秒△PCQ的面积为△ACB的面积的![]() ?
?
(2)经过几秒,△PCQ与△ACB相似?
(3)如图2,设CD为△ACB的中线,那么在运动的过程中,PQ与CD有可能互相垂直吗?若有可能,求出运动的时间;若没有可能,请说明理由.

参考答案:
【答案】(1) 2秒或4秒,(2) ![]() 秒或
秒或![]() 秒;(3)有可能.经过
秒;(3)有可能.经过![]() 秒,PQ⊥CD.
秒,PQ⊥CD.
【解析】试题分析:(1)设PC=2xm,CQ=(6﹣x)m,依照题意列一元二次方程,解方程.
(2)设运动时间为ts,△PCQ与△ACB相似,对应边成比例,列方程,解方程.
(3)假设垂直,△PCQ∽△BCA,列方程,解方程.
试题解析:
(1)设经过x秒△PCQ的面积为△ACB的面积的![]() ,
,
由题意得:PC=2xm,CQ=(6﹣x)m,
则![]() ×2x(6﹣x)=
×2x(6﹣x)=![]() ×
×![]() ×8×6,
×8×6,
解得:x=2或x=4.
故经过2秒或4秒,△PCQ的面积为△ACB的面积的![]() ;
;
(2)设运动时间为ts,△PCQ与△ACB相似.
当△PCQ与△ACB相似时,则有![]() 或
或![]() ,
,
所以![]() 或
或![]() ,
,
解得t=![]() ,或t=
,或t=![]() .
.
因此,经过![]() 秒或
秒或![]() .秒,△OCQ与△ACB相似;
.秒,△OCQ与△ACB相似;
( 3)有可能.
由勾股定理得AB=10.
∵CD为△ACB的中线,
∴∠ACD=∠A,∠BCD=∠B,
又PQ⊥CD,
∴∠CPQ=∠B,
∴△PCQ∽△BCA,
∴![]() ,
,![]() ,
,
解得y=![]() .
.
因此,经过![]() 秒,PQ⊥CD.
秒,PQ⊥CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为线段
为线段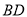 上一动点,分别过点
上一动点,分别过点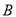 、
、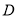 作
作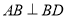 ,
,  ,连接
,连接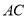 、
、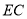 ,已知
,已知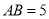 ,
,  ,
, 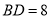 ,设
,设 .
.(1)用含
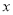 的代数式表示
的代数式表示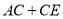 的长;
的长;(2)请问点
 在什么位置时,
在什么位置时, 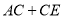 的值最小,求出这个最小值;
的值最小,求出这个最小值;(3)根据(2)中的规律和结论,构图求出代数式
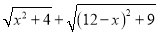 的最小值.
的最小值.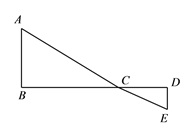
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=
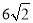 米,背水坡CD的坡度i=1:
米,背水坡CD的坡度i=1: 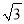 (i为DF与FC的比值),则背水坡CD的坡长为_______米.
(i为DF与FC的比值),则背水坡CD的坡长为_______米.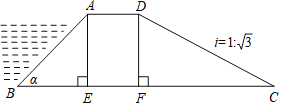
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在四边形ABCD中,∠D=37°,点E是BC边上一点,沿AE折叠,点B落在AD上B′处,若B′E∥CD,则∠B=_________°.

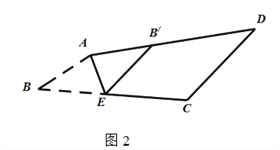
(2)如图2,在四边形ABCD中,AB∥CD,点E是BC边上一点,沿AE折叠,点B落在AD上B′处,点F是BC边上一点,沿DF折叠,点C落在AD上C′处.B′E与C′F有何位置关系?为什么?
(3)如图3,在四边形ABCD中,∠B=∠D=90°,点E是BC边上一点,沿AE折叠,点B落在AD上B′处,点F是AD边上一点,沿CF折叠,点D落在BC上D′处.试问:AE与CF有何位置关系?说明理由.

(4)在四边形ABCD中,点E是BC边上一点,沿AE折叠.
①若点B落在四边形ABCD内B′处(如图4),则∠1,∠2,∠BAD,∠B之间的数量关系为________.
②若点B落在四边形ABCD外B′处(如图5),则∠1,∠2,∠BAD,∠B之间的数量关系为 ______.

-
科目: 来源: 题型:
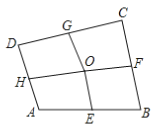
查看答案和解析>>【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别是4、5、8,则四边形DHOG的面积是________.
-
科目: 来源: 题型:
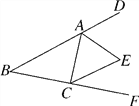
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,△ABC的外角∠DAC和∠ACF的平分线交于点E,求∠AEC的度数.
-
科目: 来源: 题型:
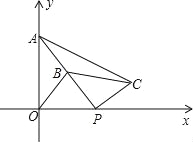
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(0,2),点P(t,0)在x轴上,B是线段PA的中点.将线段PB绕着点P顺时针方向旋转90°,得到线段PC,连结OB、BC.
(1)判断△PBC的形状,并简要说明理由;
(2)当t>0时,试问:以P、O、B、C为顶点的四边形能否为平行四边形?若能,求出相应的t的值?若不能,请说明理由;
(3)当t为何值时,△AOP与△APC相似?
相关试题

