【题目】如图,己知![]() ,
,![]() .
.
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() 平分
平分![]() ,
,![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

参考答案:
【答案】(1)AC∥EF,理由见解析;(2)∠BAD=50°
【解析】
(1)结论:AC∥EF.先证明∠CAD=∠ACE,再根据同旁内角互补两直线平行即可证明;
(2)先根据角平分线的定义求出∠ACD=∠ACE=40°,进而可求出∠CAD的值,再证明∠BAC=∠AFE=90°即可解决问题.
解:(1)结论:AC∥EF.
理由:∵![]() ,
,
∴AD//CE,
∴∠CAD=∠ACE,
∵![]() ,
,
∴![]() ,
,
∴AC∥EF;
(2)∵![]() 平分
平分![]() ,
,![]() ,
,
∴∠ACD=∠ACE=40°,
∵∠CAD=∠ACE,
∴∠CAD=40°,
∵AD∥EC,AE⊥EC,
∴∠BAC=∠AFE=90°,
∴∠BAD=90°-40°=50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(2,m)是第一象限内一点,连接OA,将OA绕点A逆时针旋转90°得到线段AB,若反比例函数y=
 (x>0)的图象恰好同时经过点A、B,则k的值为 .
(x>0)的图象恰好同时经过点A、B,则k的值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中, ,点
,点 在边
在边 上,且
上,且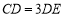 ,将
,将 沿
沿 对折至
对折至 ,延长
,延长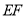 交边
交边 于点
于点 ,连接
,连接 ,
, ,则下列结论:①
,则下列结论:① ≌
≌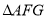 ;②
;② ;③
;③ ;④
;④ ,其中正确的个数是( )个
,其中正确的个数是( )个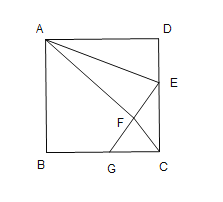
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
①
 ;②
;② ;③
;③ ;…
;…根据上述式子的规律,解答下列问题:
(1)第④个等式为 ;
(2)写出第
 个等式,并验证其正确性.
个等式,并验证其正确性. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明去文具店买文具,他与售货员的对话如下:
小明:你好.我要购买5支黑色水笔和3本笔记本.
售货员:好的.那你应该付34元.
小明:我把两种文具的单价弄反了,以为要付46元.
(1)求小明所购买的黑色水笔和笔记本的单价;
(2)如果小红也去购买同样的黑色水笔和笔记本,预算费用不超过88元,并且购买笔记本的数量要比购买黑色水笔的数量多1,那么小红最多能购买多少本笔记本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强学生的爱国意识,某中学举办“爱我中华”朗诵比赛,全校学生都参加,并对表现优异的学生进行表彰,设置一、二、三等奖和进步奖共四个奖项,赛后,校统计小组随机抽取了九年级两个班级,并将这两个班的获奖情况绘制成以下两幅不完整的统计图.
请根据图中的信息,解答下列问题:
(1)求本次调查抽取的学生人数,并补全条形统计图;
(2)在扇形统计图中,表示“三等奖”的扇形所对应的圆心角度数是 72 °.
(3)若该校共有2600名学生,试估计得奖的学生人数.
相关试题

