【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
参考答案:
【答案】(1)
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | 85 | 85 |
高中部 | 85 | 80 | 100 |
(2)初中部成绩好些(3)初中代表队选手成绩较为稳定
【解析】解:(1)填表如下:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | 85 | 85 |
高中部 | 85 | 80 | 100 |
(2)初中部成绩好些。
∵两个队的平均数都相同,初中部的中位数高,
∴在平均数相同的情况下中位数高的初中部成绩好些。
(3)∵![]() ,
,
![]() ,
,
∴![]() <
<![]() ,因此,初中代表队选手成绩较为稳定。
,因此,初中代表队选手成绩较为稳定。
(1)根据成绩表加以计算可补全统计表.根据平均数、众数、中位数的统计意义回答。
(2)根据平均数和中位数的统计意义分析得出即可。
(3)分别求出初中、高中部的方差比较即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形
 中,
中, ,点E、F分别在边AB、AC上,将
,点E、F分别在边AB、AC上,将 沿着直线EF折叠,使得A点恰好落在BC边上的D点处,且
沿着直线EF折叠,使得A点恰好落在BC边上的D点处,且 .
. 求证:四边形AFDE是菱形.
求证:四边形AFDE是菱形. 若
若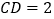 ,
,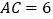 ,求线段ED的长度.
,求线段ED的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8,则AC的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与证明:如图,把一个含
 角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、
角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、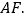 其中AC与EF交于点N,取AF中点M,连接MD、MN.
其中AC与EF交于点N,取AF中点M,连接MD、MN.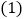 求证:
求证: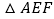 是等腰三角形;
是等腰三角形;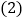 在
在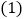 的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.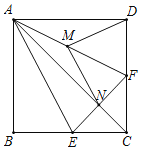
-
科目: 来源: 题型:
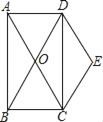
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
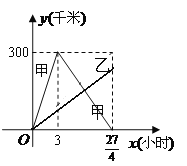
查看答案和解析>>【题目】已知:甲、乙两车分别从相距300千米的 A,B两地同时出发相向而行,其中甲到 B地后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离 y(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)当它们行驶到与各自出发地的距离相等时,用了
 小时,求乙车离出发地的距离 y(千米)与行驶时间 x(小时)之间的函数关系式;
小时,求乙车离出发地的距离 y(千米)与行驶时间 x(小时)之间的函数关系式; (3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
相关试题

