【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y= ![]() (x﹥0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
(x﹥0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 . 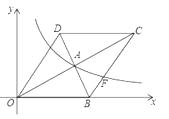
参考答案:
【答案】(12,![]() )
)
【解析】过点D作DM⊥x轴于点M,过点F作FE⊥x轴于点E,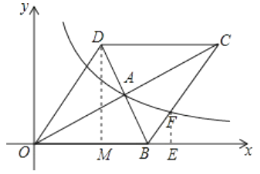
∵D(6,8),
∴OD=![]() =10,
=10,
又∵四边形OBCD是菱形,
∴OB=OD=10,AB=AD,OD∥BC,
∴B(10,0),
∵OM=6,DM=8,
∴A(8,4)
∵A在反比例函数上,
∴k=4×8=32,
又∵OD∥BC,
∴∠DOM=∠FBE,
∴tan∠DOM=![]() =
=![]() =
=![]() =tan∠FBE=
=tan∠FBE=![]() ,
,
∴设FE=4x,BE=3x,
∴F(10+3x,4x),
∵F在反比例函数上,
∴32=(10+3x)×4x,
∴3x2+10x-8=0,
∴x1=![]() ,x2=-4(舍去)
,x2=-4(舍去)
∴F(12,![]() ),
),
所以答案是:(12,![]() ).
).
【考点精析】本题主要考查了勾股定理的概念和菱形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=ADAB;④ABCD=ADCB,能满足△ADC与△ACB相似的条件是( )

A.①、②、③ B.①、③、④ C.②、③、④ D.①、②、④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,∠BAD=90°,对角线BD⊥DC, 如果AD=4,BC=9,则BD的长=___________ 。
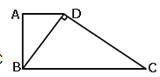
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明将两块完全相同的直角三角形纸片的直角顶点C叠放在一起,若保持△BCD不动,将△ACE绕直角顶点C旋转.
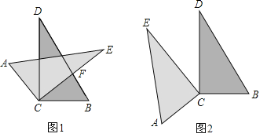
(1)如图1,如果CD平分∠ACE,那么CE是否平分∠BCD?答:______(填写“是”或“否”);
(2)如图1,若∠DCE=35,则∠ACB=______;若∠ACB=140,则∠DCE=______;
(3)当△ACE绕直角顶点C旋转到如图1的位置时,猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)当△ACE绕直角顶点C旋转到如图2的位置时,上述关系是否依然成立,请说明理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1) x22x7=0
x22x7=0
(2) 2(x1)2=1x
2(x1)2=1x -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学本学期11次考试的测试成绩如下:
甲
98
100
100
90
96
91
89
99
100
100
93
乙
98
99
96
94
95
92
92
98
96
99
97
(1) 他们的平均成绩和方差各是多少?
(2) 分析他们的成绩各有什么特点?
(3) 现要从两人中选一人参加比赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这次比赛?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=90
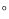 ,射线OC绕点O从OA位置开始,以每秒4
,射线OC绕点O从OA位置开始,以每秒4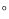 的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1
的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1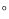 的速度逆时针方向旋转. 当OC与OA成180
的速度逆时针方向旋转. 当OC与OA成180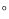 时,OC与OD同时停止旋转.
时,OC与OD同时停止旋转.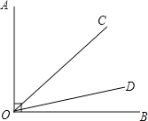
(1)当OC旋转10秒时,∠COD=___.
(2)当OC与OD的夹角是30
 时,求旋转的时间.
时,求旋转的时间.(3)当OB平分∠COD时,求旋转的时间.
相关试题

