搜索
【题目】甲、乙两位同学本学期11次考试的测试成绩如下：
甲 | 98 | 100 | 100 | 90 | 96 | 91 | 89 | 99 | 100 | 100 | 93 |
乙 | 98 | 99 | 96 | 94 | 95 | 92 | 92 | 98 | 96 | 99 | 97 |
（1） 他们的平均成绩和方差各是多少？
（2） 分析他们的成绩各有什么特点？
（3） 现要从两人中选一人参加比赛，历届比赛成绩表明，平时成绩达到98分以上才可能进入决赛，你认为应选谁参加这次比赛？为什么？
参考答案：
【答案】(1)
甲
(分)，乙 (分)；S2甲 
S2乙 
(2)由以上所求得出：两人平均成绩相同，甲的标准差大于乙的标准差，故甲的成绩不稳定；
(3)应选甲谁参加这项竞赛.
【解析】
（1）根据平均数的定义进而求出；利用方差的公式分别求得甲、乙两人的方差；
（2）利用标准差的意义进而分析得出即可；
（3）利用达到98分以上才可能进入决赛，结合两人超过98分的次数即可得出答案．
(1)甲
(分)，
乙
(分)；
S2甲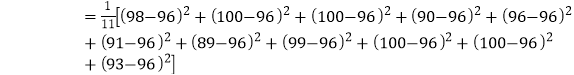
S2乙
(2)由以上所求得出：两人平均成绩相同，甲的标准差大于乙的标准差，故甲的成绩不稳定；
(3)∵历届比赛成绩表明，平时成绩达到98分以上才可能进入决赛，甲的成绩有6次超过98分，乙的成绩有4次超过98分，
∴应选甲谁参加这项竞赛.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，小明将两块完全相同的直角三角形纸片的直角顶点C叠放在一起，若保持△BCD不动，将△ACE绕直角顶点C旋转．
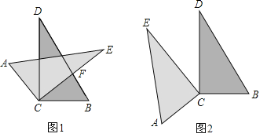
（1）如图1，如果CD平分∠ACE，那么CE是否平分∠BCD?答：______（填写“是”或“否”）；
（2）如图1，若∠DCE=35，则∠ACB=______；若∠ACB=140，则∠DCE=______；
（3）当△ACE绕直角顶点C旋转到如图1的位置时，猜想∠ACB与∠DCE的数量关系，并说明理由；
（4）当△ACE绕直角顶点C旋转到如图2的位置时，上述关系是否依然成立，请说明理由；
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，菱形OBCD的边OB在x轴正半轴上，反比例函数y=
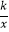（x﹥0）的图象经过该菱形对角线的交点A，且与边BC交于点F．若点D的坐标为（6，8），则点F的坐标是 ．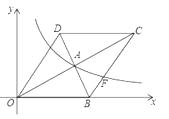 
-
科目： 来源： 题型：
查看答案和解析>>【题目】解下列方程：
（1）
x22x7=0
（2）2（x1）2=1x -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠AOB=90
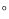，射线OC绕点O从OA位置开始，以每秒4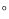的速度顺时针方向旋转；同时，射线OD绕点O从OB位置开始，以每秒1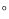的速度逆时针方向旋转． 当OC与OA成180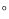时，OC与OD同时停止旋转．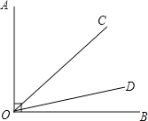
（1）当OC旋转10秒时，∠COD=___．
（2）当OC与OD的夹角是30
时，求旋转的时间．（3）当OB平分∠COD时，求旋转的时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC，∠C=90°，∠ABC=40°，按以下步骤作图：
①以点A为圆心，小于AC的长为半径．画弧，分别交AB、AC于点E、F；
②分别以点E、F为圆心，大于
EF的长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D，则∠ADC的度数为________．
【答案】65°
【解析】由题意可知，所作的射线AG是∠BAC的角平分线.
∵在△ABC中，∠C=90°，∠ABC=40°，
∴∠BAC=180°-90°-40°=50°，
∴∠CAD=
∠BAC=25°，∴∠ADC=180°-90°-25°=65°.
【题型】填空题
【结束】
13【题目】如图所示，已知线段AB，∠α，∠β，分别过A、B作∠CAB=∠α，∠CBA=∠β．（不写作法，保留作图痕迹）
-
科目： 来源： 题型：
查看答案和解析>>【题目】填写推理的依据。
（1）已知：AB∥CD，AD∥BC。求证：∠B=∠D。
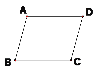
证明：∵AB∥CD，AD∥BC（ 已知 ）
∴∠A+∠B=180，∠A+∠D=180°（_______________________________）
∴∠B=∠D （___________________________）
（2）已知：DF∥AC，∠A=∠F。求证：AE∥BF。
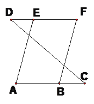
证明：∵DF∥AC （已知）
∴∠FBC=∠_______（_______________________________）
∵∠A=∠F（已知）
∴∠A=∠FBC （____________________）
∴AE∥FB （_____________________________）
相关试题
