【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且![]() .连接PB,试探究PA,PB,PC满足的等量关系.
.连接PB,试探究PA,PB,PC满足的等量关系.
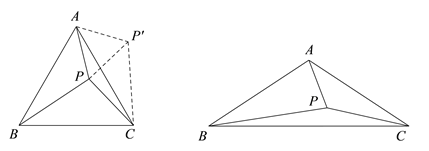
图1 图2
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到![]() ,连接
,连接![]() ,如图1所示.
,如图1所示.
由![]() ≌
≌![]() 可以证得
可以证得![]() 是等边三角形,再由
是等边三角形,再由![]() 可得∠APC的大小为 度,进而得到
可得∠APC的大小为 度,进而得到![]() 是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
(2)如图2,当α=120°时,请参考(1)中的方法,探究PA,PB,PC满足的等量关系,并给出证明;
(3)PA,PB,PC满足的等量关系为 .
参考答案:
【答案】(1)150, ![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】试题分析:(1)根据旋转变换的性质得到△PAP′为等边三角形,得到∠P′PC=90°,根据勾股定理解答即可;
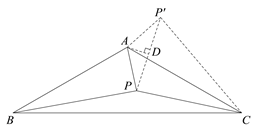
(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,作AD⊥PP′于D,根据余弦的定义得到PP′=![]() PA,根据勾股定理解答即可;
PA,根据勾股定理解答即可;
(3)与(2)类似,根据旋转变换的性质、勾股定理和余弦、正弦的关系计算即可.
试题解析:
解:(1)∵△ABP≌△ACP′,
∴AP=AP′,
由旋转变换的性质可知,∠PAP′=60°,P′C=PB,
∴△PAP′为等边三角形,
∴∠APP′=60°,
∵∠PAC+∠PCA=![]() ×60° =30°,
×60° =30°,
∴∠APC=150°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∴PA2+PC2=PB2,
故答案为:150,PA2+PC2=PB2;
(2)如图,作![]() °,使
°,使![]() ,连接
,连接![]() ,
, ![]() .过点A作AD⊥
.过点A作AD⊥![]() 于D点.
于D点.
∵![]() °,
°,
即![]() ,
,
∴![]() .
.
∵AB=AC, ![]() ,
,
∴![]() .
.
∴![]() ,
, ![]() °.
°.
∵AD⊥![]() ,
,
∴![]() °.
°.
∴在Rt ![]() 中,
中, ![]() .
.
∴![]() .
.
∵![]() °,
°,
∴![]() °.
°.
∴![]() °.
°.
∴在Rt ![]() 中,
中, ![]() .
.
∴![]() ;
;
(3)如图2,与(2)的方法类似,
作将△ABP绕点A逆时针旋转α得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=α,P′C=PB,
∴∠APP′=90°-![]() ,
,
∵∠PAC+∠PCA=![]() ,
,
∴∠APC=180°-![]() ,
,
∴∠P′PC=(180°-![]() )-(90°-
)-(90°-![]() )=90°,
)=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=90°-![]() ,
,
∴PD=PAcos(90°-![]() )=PAsin
)=PAsin![]() ,
,
∴PP′=2PAsin![]() ,
,
∴4PA2sin2![]()
故答案为:4PA2sin2![]() +PC2=PB2.
+PC2=PB2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
 的性质.
的性质.(1)先从简单情况开始探究:
① 当函数为
 时,
时,  随
随 增大而 (填“增大”或“减小”);
增大而 (填“增大”或“减小”);② 当函数为
 时,它的图象与直线
时,它的图象与直线 的交点坐标为 ;
的交点坐标为 ;(2)当函数为
 时,
时,下表为其y与x的几组对应值.
x
…

0
1

2

3
4

…
y
…


1

2

3
7

…

①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
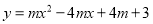 的顶点为A.
的顶点为A.(1)求点A的坐标;

(2)将线段
 沿
沿 轴向右平移2个单位得到线段
轴向右平移2个单位得到线段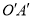 .
.①直接写出点
 和
和 的坐标;
的坐标;②若抛物线
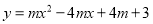 与四边形
与四边形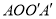 有且只有两个公共点,结合函数的图象,求
有且只有两个公共点,结合函数的图象,求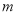 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一个“有理数转换器”(箭头是数进入转换器的路径,方框是对进入的数进行转换的转换器)
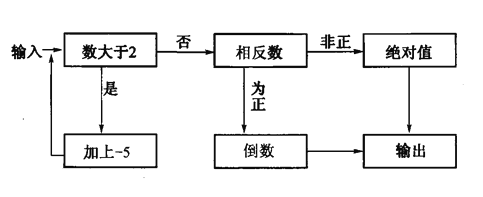
(1)当小明输入-3、
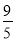 、0.4这三个数时,三次输出的结果分别是 、_______、 .
、0.4这三个数时,三次输出的结果分别是 、_______、 .(2)你认为当输入 时(写出2个即可),其输出结果是0?
(3)你认为这个“有理数转换器”不可能输出 数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD的周长为24,∠ABC=60°,以AB为腰在菱形外作底角为45°的等腰△ABE,连结AC,CE,则△ACE的面积为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:点P为△ABC内部或边上的点,若满足△PAB,△PBC,△PAC至少有一个三角形与△ABC相似(点P不与△ABC顶点重合),则称点P为△ABC的自相似点.

例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
在平面直角坐标系xOy中,
(1)点A坐标为(
 ,
,  ), AB⊥x轴于B点,在E(2,1),F (
), AB⊥x轴于B点,在E(2,1),F ( ,
,  ),G (
),G ( ,
,  ),这三个点中,其中是△AOB的自相似点的是 (填字母);
),这三个点中,其中是△AOB的自相似点的是 (填字母);(2)若点M是曲线C:
 (
( ,
,  )上的一个动点,N为x轴正半轴上一个动点;
)上的一个动点,N为x轴正半轴上一个动点; 图2
图2① 如图2,
 ,M点横坐标为3,且NM = NO,若点P是△MON的自相似点,求点P的坐标;
,M点横坐标为3,且NM = NO,若点P是△MON的自相似点,求点P的坐标;②若
 ,点N为(2,0),且△MON的自相似点有2个,则曲线C上满足这样条件的点M共有 个,请在图3中画出这些点(保留必要的画图痕迹).
,点N为(2,0),且△MON的自相似点有2个,则曲线C上满足这样条件的点M共有 个,请在图3中画出这些点(保留必要的画图痕迹).
-
科目: 来源: 题型:
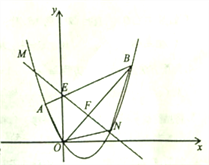
查看答案和解析>>【题目】(12分)如图,平面直角坐标系
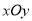 中点
中点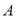 的坐标为
的坐标为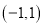 ,点
,点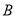 的坐标为
的坐标为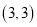 ,抛物线经过
,抛物线经过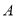 、
、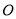 、
、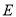 三点,连接
三点,连接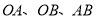 ,线段
,线段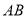 交
交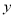 轴于点
轴于点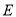 .
.
(1)求点
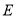 的坐标;
的坐标;(2)求抛物线的函数解析式;
(3)点
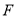 为线段
为线段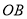 上的一个动点(不与点
上的一个动点(不与点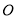 、
、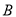 重合),直线
重合),直线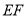 与抛物线交于
与抛物线交于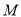 、
、 两点(点
两点(点 在
在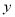 轴右侧),连接
轴右侧),连接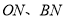 ,当四边形
,当四边形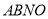 的面积最大时,求点
的面积最大时,求点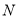 的坐标并求出四边形
的坐标并求出四边形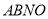 面积的最大值.
面积的最大值.
相关试题

