【题目】在平面直角坐标系xOy中,抛物线![]() 的顶点为A.
的顶点为A.
(1)求点A的坐标;

(2)将线段![]() 沿
沿![]() 轴向右平移2个单位得到线段
轴向右平移2个单位得到线段![]() .
.
①直接写出点![]() 和
和![]() 的坐标;
的坐标;
②若抛物线![]() 与四边形
与四边形![]() 有且只有两个公共点,结合函数的图象,求
有且只有两个公共点,结合函数的图象,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)(2,3)(2)![]() (2,0),
(2,0), ![]() (4,3)(3)
(4,3)(3)![]()
【解析】试题分析:(1)将抛物线解析式配成顶点式,即可得出顶点坐标;
(2)根据平移的性质即可得出结论;
(3)结合图象,判断出抛物线和四边形AOO'A'只有两个公共点的分界点即可得出结论.
试题解析:
解:(1)∵y=mx2-4mx+4m+3=m(x2-4x+4)+3=m(x-2)2+3,
∴抛物线的顶点A的坐标为(2,3).
(2)由(1)知,A(2,3),
∵线段OA沿x轴向右平移2个单位长度得到线段O′A′.
∴A'(4,3),O'(2,0);
(3)如图,
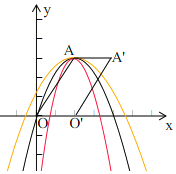
∵抛物线y=mx2-4mx+4m+3与四边形AOO′A′有且只有两个公共点,
∴m<0.
由图象可知,抛物线是始终和四边形AOO'A'的边O'A'相交,
∴抛物线已经和四边形AOO′A′有两个公共点,
∴将(0,0)代入y=mx2-4mx+4m+3中,得m=![]() .
.
∴![]() <m<0.
<m<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=3,BC=6,P为BC边上一点,△APD为等腰三角形.
(1)小明画出了一个满足条件的△APD,其中PA=PD,如图1所示,则tan
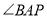 的值为 ;
的值为 ;(2)请你在图2中再画出一个满足条件的△APD(与小明的不同),并求此时tan
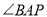 的值.
的值.

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD的外角∠DAF的平分线.

(1)求证:AM是⊙O的切线;
(2)若∠D = 60°,AD = 2,射线CO与AM交于N点,请写出求ON长的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
 的性质.
的性质.(1)先从简单情况开始探究:
① 当函数为
 时,
时,  随
随 增大而 (填“增大”或“减小”);
增大而 (填“增大”或“减小”);② 当函数为
 时,它的图象与直线
时,它的图象与直线 的交点坐标为 ;
的交点坐标为 ;(2)当函数为
 时,
时,下表为其y与x的几组对应值.
x
…

0
1

2

3
4

…
y
…


1

2

3
7

…

①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一个“有理数转换器”(箭头是数进入转换器的路径,方框是对进入的数进行转换的转换器)
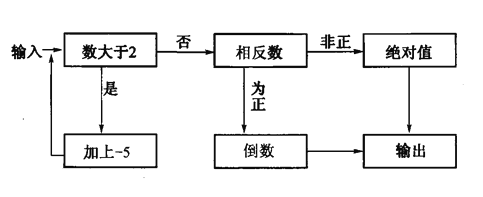
(1)当小明输入-3、
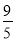 、0.4这三个数时,三次输出的结果分别是 、_______、 .
、0.4这三个数时,三次输出的结果分别是 、_______、 .(2)你认为当输入 时(写出2个即可),其输出结果是0?
(3)你认为这个“有理数转换器”不可能输出 数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且
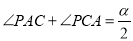 .连接PB,试探究PA,PB,PC满足的等量关系.
.连接PB,试探究PA,PB,PC满足的等量关系.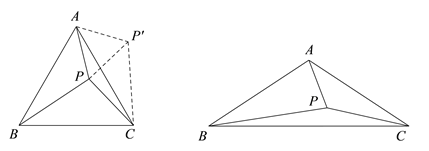
图1 图2
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到
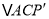 ,连接
,连接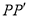 ,如图1所示.
,如图1所示.由
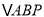 ≌
≌ 可以证得
可以证得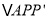 是等边三角形,再由
是等边三角形,再由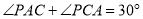 可得∠APC的大小为 度,进而得到
可得∠APC的大小为 度,进而得到 是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;(2)如图2,当α=120°时,请参考(1)中的方法,探究PA,PB,PC满足的等量关系,并给出证明;
(3)PA,PB,PC满足的等量关系为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD的周长为24,∠ABC=60°,以AB为腰在菱形外作底角为45°的等腰△ABE,连结AC,CE,则△ACE的面积为___________.
相关试题

