【题目】如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为菱形,则应添加的条件是( )

A.AB∥DCB.AD=BCC.AC⊥BDD.AC=BD
参考答案:
【答案】D
【解析】
连接AC,BD,根据三角形中位线的性质得到EF∥AC,EF=![]() AC;HG∥AC,HG=
AC;HG∥AC,HG=![]() AC,即有四边形EFGH为平行四边形,当AB∥DC和AB=DC,只能判断四边形EFGH为平行四边形;当AC⊥BD,只能判断四边形EFGH为矩形;当AC=BD,可判断四边形EFGH为菱形.
AC,即有四边形EFGH为平行四边形,当AB∥DC和AB=DC,只能判断四边形EFGH为平行四边形;当AC⊥BD,只能判断四边形EFGH为矩形;当AC=BD,可判断四边形EFGH为菱形.
解:∵E、F、G、H为四边形ABCD各中点,
∴EF∥AC,EF=![]() AC;HG∥AC,HG=
AC;HG∥AC,HG=![]() AC,
AC,
∴四边形EFGH为平行四边形,
要使四边形EFGH为菱形,则EF=EH,
而EH=![]() BD,
BD,
∴AC=BD.
当AB∥DC和AB=DC,只能判断四边形EFGH为平行四边形,故A、B选项错误;
当AC⊥BD,只能判断四边形EFGH为矩形,故C选项错误;
当AC=BD,可判断四边形EFGH为菱形,故D选项正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】依据给定的条件,求一次函数的表达式.
(1)已知一次函数的图象如图所示,求此一次函数的表达式,并判断点(6,5)是否在此函数图象上;
(2)已知直线y=kx+b平行于直线y=3x+4,且过点(1,2),求此直线的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=﹣x+m经过点A(2,0),交y轴于点B.点D为x轴上一点,且S△ADB=1.

(1)求m的值;
(2)求线段OD的长;
(3)当点E在直线AB上(点E与点B不重合),且∠BDO=∠EDA,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点M(k﹣1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(k﹣1)x+k的图象不经过第( )象限.
A.一B.二C.三D.四
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 分别是
分别是 的高和中线,
的高和中线, ,
, ,
, ,
, .
.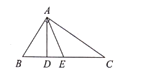
求:(1)
 的长;
的长;(2)
 的面积;
的面积;(3)
 和
和 的周长的差.
的周长的差. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点E是正方形ABCD中AD边上的一动点,连结BE,作∠BEG=∠BEA交CD于G,再以B为圆心作
 ,连结BG.
,连结BG.(1)求证:EG与
 相切.
相切.(2)求∠EBG的度数.
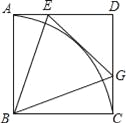
相关试题

