【题目】在平面直角坐标系xOy中,直线y=﹣x+m经过点A(2,0),交y轴于点B.点D为x轴上一点,且S△ADB=1.

(1)求m的值;
(2)求线段OD的长;
(3)当点E在直线AB上(点E与点B不重合),且∠BDO=∠EDA,求点E的坐标.
参考答案:
【答案】(1)2;(2)OD=1或OD=3;(3)点E的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)把点A的坐标代入直线解析式进行计算即可求出m的值;
(2)根据三角形的面积求出AD的长度,然后分点D在点A的左边与右边两种情况得到点D的坐标,再根据两点间的距离得到OD的长度;
(3)找出点B关于x轴的对称点B′,根据轴对称性作出∠BDO=∠EDA从而确定出点E的位置,再分点D的两种情况利用待定系数法求出直线B′D的解析式,然后联立直线AB的解析式,解方程组即可得到点E的坐标.
(1)∵直线y=﹣x+m经过点A(2,0),
∴0=﹣2+m,
∴m=2;
(2)∵直线y=﹣x+2交y轴于点B,
∴点B的坐标为(0,2),
∴OB=2,
∵S△ADB=![]() ADOB=1,
ADOB=1,
∴AD=1,
∵点A的坐标为(2,0),
∴点D的坐标为(1,0)或(3,0),
∴OD=1或OD=3;
(3)①当点D的坐标为(1,0)时,如图所示,
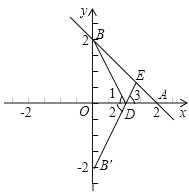
取点B′(0,﹣2),连接B′D并延长,交直线BA于点E.
∵OB=OB′,AO⊥BB′于O,
∴OD为BB′的垂直平分线.
∴DB=DB′,
∴∠1=∠2.
又∵∠2=∠3,
∴∠1=∠3,
设直线B′D的解析式为y=kx﹣2(k≠0),
∵直线B′D经过点D(1,0),
∴0=k﹣2,
∴k=2,
∴直线B′D的解析式为y=2x﹣2,
联立得![]() ,
,
解得![]() ,
,
∴点E的坐标为(![]() ,
,![]() );
);
②当点D的坐标为(3,0)时,如图所示,
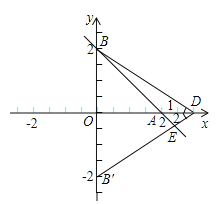
取点B′(0,﹣2),连接B′D,交直线BA于点E,
同①的方法,可得∠1=∠2,直线B′D的解析式为y=![]() x﹣2,
x﹣2,
联立得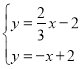 ,
,
解得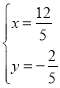 ,
,
∴点E的坐标为(![]() ,
,![]() ),
),
综上所述,点E的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
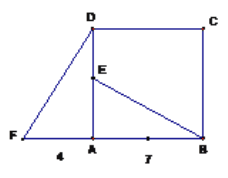
查看答案和解析>>【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7.
(1)旋转中心是点 ,旋转了 度,DE的长度是 ;
(2)BE与DF的关系如何? 请说明理由.(提示:延长BE交DF于点G)
-
科目: 来源: 题型:
查看答案和解析>>【题目】依据给定的条件,求一次函数的表达式.
(1)已知一次函数的图象如图所示,求此一次函数的表达式,并判断点(6,5)是否在此函数图象上;
(2)已知直线y=kx+b平行于直线y=3x+4,且过点(1,2),求此直线的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为菱形,则应添加的条件是( )

A.AB∥DCB.AD=BCC.AC⊥BDD.AC=BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点M(k﹣1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(k﹣1)x+k的图象不经过第( )象限.
A.一B.二C.三D.四
-
科目: 来源: 题型:
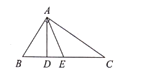
查看答案和解析>>【题目】如图,已知
 分别是
分别是 的高和中线,
的高和中线, ,
, ,
, ,
, .
.
求:(1)
 的长;
的长;(2)
 的面积;
的面积;(3)
 和
和 的周长的差.
的周长的差.
相关试题

