【题目】如图,已知![]() 分别是
分别是![]() 的高和中线,
的高和中线,![]() ,
,![]() ,
,![]() ,
,![]() .
.
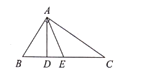
求:(1)![]() 的长;
的长;
(2)![]() 的面积;
的面积;
(3)![]() 和
和![]() 的周长的差.
的周长的差.
参考答案:
【答案】(1) ![]() 的长度为
的长度为![]() ;(2)
;(2) ![]() 的面积是
的面积是![]() ;(3)
;(3) ![]() 和
和![]() 的周长的差是
的周长的差是![]()
【解析】
(1)利用“面积法”来求线段AD的长度;
(2)根据△AEC与△ABE是等底同高的两个三角形,它们的面积相等,求解即可.
(3)由于AE是中线,那么BE=CE,于是△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE),化简可得△ACE的周长-△ABE的周长=AC-AB,易求其值.
(1)∵![]() ,
,![]() 是边
是边![]() 上的高,
上的高,
∴![]() ,
,
∴![]() ,
,
即![]() 的长度为
的长度为![]() ;
;
(2)∵![]() 是直角三角形,
是直角三角形,![]() ,
,
∴![]() ,
,
又∵![]() 是边
是边![]() 的中线,
的中线,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 的面积是
的面积是![]() ;
;
(3)∵![]() 为
为![]() 边上的中线,∴
边上的中线,∴![]() ,
,
∴![]() 的周长-
的周长-![]() 的周长
的周长![]()
![]() ,
,
即![]() 和
和![]() 的周长的差是
的周长的差是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=﹣x+m经过点A(2,0),交y轴于点B.点D为x轴上一点,且S△ADB=1.

(1)求m的值;
(2)求线段OD的长;
(3)当点E在直线AB上(点E与点B不重合),且∠BDO=∠EDA,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为菱形,则应添加的条件是( )

A.AB∥DCB.AD=BCC.AC⊥BDD.AC=BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点M(k﹣1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(k﹣1)x+k的图象不经过第( )象限.
A.一B.二C.三D.四
-
科目: 来源: 题型:
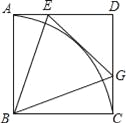
查看答案和解析>>【题目】已知:如图,点E是正方形ABCD中AD边上的一动点,连结BE,作∠BEG=∠BEA交CD于G,再以B为圆心作
 ,连结BG.
,连结BG.(1)求证:EG与
 相切.
相切.(2)求∠EBG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( )

A.y=
 x+5B.y=
x+5B.y= x+5C.y=
x+5C.y=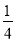 x+5D.y=
x+5D.y= x+5
x+5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,点M、N分别在AD,BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC=_____.

相关试题

