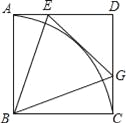
【题目】已知:如图,点E是正方形ABCD中AD边上的一动点,连结BE,作∠BEG=∠BEA交CD于G,再以B为圆心作![]() ,连结BG.
,连结BG.
(1)求证:EG与![]() 相切.
相切.
(2)求∠EBG的度数.
参考答案:
【答案】(1)证明见解析;(2)45°.
【解析】试题分析:(1)过点B作BF⊥EG,垂足为F,先证得△ABE≌△FBE,得出BF=BA,根据切线的判定即可证得结论;
(2)由△ABE≌△FBE得出∠FBE=∠ABE=![]() ∠ABF,然后根据切线长定理得出GF=GC,进而证得∠FBG=∠CBG=
∠ABF,然后根据切线长定理得出GF=GC,进而证得∠FBG=∠CBG=![]() ∠FBC,从而得出∠EBG=
∠FBC,从而得出∠EBG=![]() ∠ABC=45°.
∠ABC=45°.
试题解析:(1)过点B作BF⊥EG,垂足为F,
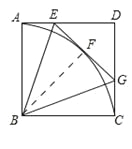
∴∠BFE=90°
∵四边形ABCD是正方形∴∠A=90°,∴∠BFE=∠A,
∵∠BEG=∠BEA,BE=BE, ∴△ABE≌△FBE, ∴BF=BA,
∵BA为![]() 的半径,∴BF为
的半径,∴BF为![]() 的半径,∴EG与
的半径,∴EG与![]() 相切;
相切;
(2)由(1)可得△ABE≌△FBE,∴∠1=∠ABE=![]() ∠ABF,
∠ABF,
∵四边形ABCD是正方形,∴∠C=∠ABC=90°,∴CD是⊙O切线,
由(1)可得EG与![]() 相切,∴GF=GC,
相切,∴GF=GC,
∵BF⊥EG,BC⊥CD,∴∠2=∠CBG=![]() ∠FBC,
∠FBC,
∴∠EBG=∠1+∠2=![]() (∠ABF+∠FBC)=
(∠ABF+∠FBC)= ![]() ∠ABC=45°
∠ABC=45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为菱形,则应添加的条件是( )

A.AB∥DCB.AD=BCC.AC⊥BDD.AC=BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点M(k﹣1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(k﹣1)x+k的图象不经过第( )象限.
A.一B.二C.三D.四
-
科目: 来源: 题型:
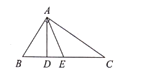
查看答案和解析>>【题目】如图,已知
 分别是
分别是 的高和中线,
的高和中线, ,
, ,
, ,
, .
.
求:(1)
 的长;
的长;(2)
 的面积;
的面积;(3)
 和
和 的周长的差.
的周长的差. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( )

A.y=
 x+5B.y=
x+5B.y= x+5C.y=
x+5C.y=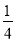 x+5D.y=
x+5D.y= x+5
x+5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,点M、N分别在AD,BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC=_____.

-
科目: 来源: 题型:
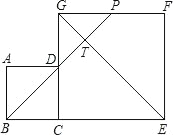
查看答案和解析>>【题目】如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为_____.
相关试题

