【题目】某校有![]() 名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
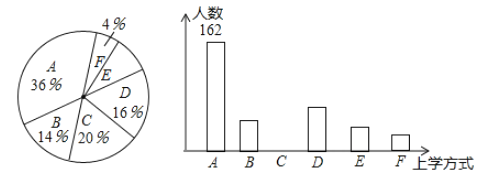
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有_____人,其中选择![]() 类的人数有_____人;
类的人数有_____人;
(2)在扇形统计图中,求![]() 类对应的扇形圆心角
类对应的扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)若将![]() 这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
参考答案:
【答案】(1)450,63;(2)![]() ,补全的条形统计图见解析;(3)该校选择“绿色出行”的学生人数为2460人.
,补全的条形统计图见解析;(3)该校选择“绿色出行”的学生人数为2460人.
【解析】
(1)根据A类学生的扇形统计图和条形统计图的信息可得参与调查的总人数,再乘以B类学生的占比可得选择B类的人数;
(2)根据扇形统计图的定义得出E类学生的占比,从而可得其圆心角的度数,根据(1)的答案和扇形统计图先求出![]() 类学生的人数,再补全条形统计图即可;
类学生的人数,再补全条形统计图即可;
(3)先求出“绿色出行”的上学方式的占比,再乘以![]() 即可.
即可.
(1)参与本次问卷调查的学生总人数为![]() (人)
(人)
选择![]() 类的人数为
类的人数为![]() (人)
(人)
故答案为:450,63;
(2)E类学生的占比为![]()
则![]() 类对应的扇形圆心角
类对应的扇形圆心角![]() 的度数为
的度数为![]()
选择C类学生的人数为![]() (人)
(人)
选择D类学生的人数为![]() (人)
(人)
选择E类学生的人数为![]() (人)
(人)
选择F类学生的人数为![]() (人)
(人)
补全条形统计图如下所示:
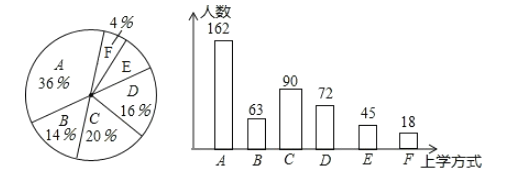
(3)由题意得:“绿色出行”的上学方式的占比为![]()
则该校选择“绿色出行”的学生人数为![]() (人)
(人)
答:该校选择“绿色出行”的学生人数为2460人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,经过原点O的抛物线
 (a≠0)与x轴交于另一点A(
(a≠0)与x轴交于另一点A( ,0),在第一象限内与直线y=x交于点B(2,t).
,0),在第一象限内与直线y=x交于点B(2,t).(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1:y=﹣
 x与反比例函数y=
x与反比例函数y= 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:(1)求反比例函数的表达式;
(2)将直线l1:y=﹣
 x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y= 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2
 ,直接写出线段BF的范围.
,直接写出线段BF的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC≤BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、点F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 的半径为 4,
的半径为 4,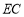 是圆的直径,点
是圆的直径,点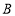 是
是 的切线
的切线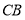 上的一个动点,连接
上的一个动点,连接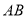 交
交 于点
于点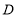 ,弦
,弦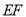 平行于
平行于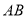 ,连接
,连接 .
. 
(1)试判断直线
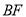 与
与 的位置关系,并说明理由;
的位置关系,并说明理由; (2)当
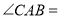 __________时,四边形
__________时,四边形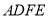 为菱形;
为菱形; (3)当
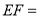 ___________时,四边形
___________时,四边形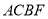 为正方形.
为正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为
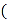

A. 1或
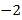 B. -
B. -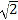 或
或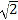 C.
C. 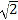 D. 1
D. 1
相关试题

