【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为![]()
![]()
A. 1或![]() B. -
B. -![]() 或
或![]() C.
C. ![]() D. 1
D. 1
参考答案:
【答案】D
【解析】
先求出二次函数的对称轴,再根据二次函数的增减性得出抛物线开口向上a>0,然后由-2≤x≤1时,y的最大值为9,可得x=1时,y=9,即可求出a.
∵二次函数y=ax2+2ax+3a2+3(其中x是自变量),
∴对称轴是直线x=-![]() =-1,
=-1,
∵当x≥2时,y随x的增大而增大,
∴a>0,
∵-2≤x≤1时,y的最大值为9,
∴x=1时,y=a+2a+3a2+3=9,
∴3a2+3a-6=0,
∴a=1,或a=-2(不合题意舍去).
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校团委计划在元且期间组织优秀团员到敬老院去服务,现选出了10名优秀团员参加服务,其中男生6人,女生4人.
 若从这10人中随机选一人当队长,求选中女生当队长的概率;
若从这10人中随机选一人当队长,求选中女生当队长的概率; 现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长
现决定从甲、乙中选一人当队长,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则选甲为队长;否则,选乙为队长 试问这个游戏公平吗?请用树状图或列表法说明理由.
试问这个游戏公平吗?请用树状图或列表法说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市政府规定:若本市企业按生产成本价提供产品给大学生销售,则政府给该企业补偿
 补偿额
补偿额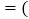 批发价
批发价 生产成本价
生产成本价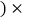 销售量
销售量 大学生小明投资销售本市企业生产的一种新型节能灯,调查发现,每月销售量
大学生小明投资销售本市企业生产的一种新型节能灯,调查发现,每月销售量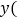 件
件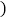 与销售单价
与销售单价 元
元 之间的关系近似满足一次函数:
之间的关系近似满足一次函数: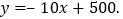 已知这种节能灯批发价为每件12元,设它的生产成本价为每件m元
已知这种节能灯批发价为每件12元,设它的生产成本价为每件m元
(1)当
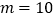 时.
时.①若第一个月的销售单价定为20元,则第一个月政府要给该企业补偿多少元?
②设所获得的利润为
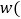 元
元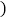 ,当销售单价定为多少元时,每月可获得最大利润?
,当销售单价定为多少元时,每月可获得最大利润?(2)物价部门规定,这种节能灯的销售单价不得超过30元
 今年三月小明获得赢利,此时政府给该企业补偿了920元,若m,x都是正整数,求m的值.
今年三月小明获得赢利,此时政府给该企业补偿了920元,若m,x都是正整数,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,点P是射线BA上的一个动点,以BP为半径的
,点P是射线BA上的一个动点,以BP为半径的 交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点
交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点 ,连结
,连结 ,
, ,设直线
,设直线 与直线BC交于点F.
与直线BC交于点F. 当点P在线段BA上时,
当点P在线段BA上时, 求证:
求证: ;
; 连结
连结 ,当
,当 时,求
时,求 的长;
的长; 连结AD,AF,当
连结AD,AF,当 恰为等边三角形时,求此时四边形
恰为等边三角形时,求此时四边形 的面积;
的面积; 当四边形
当四边形 在
在 内部时,请直接写出BP的取值范围.
内部时,请直接写出BP的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△
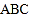 中,∠
中,∠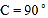 ,点
,点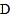 是
是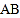 边上一点,以
边上一点,以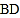 为直径的⊙
为直径的⊙ 与边
与边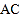 相切于点
相切于点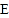 ,与边
,与边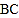 交于点
交于点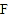 ,过点
,过点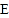 作
作 ⊥
⊥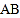 于点
于点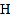 ,连接
,连接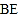 .
.(1)求证:
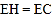 ;
;(2)若
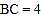 ,
, ,求
,求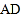 的长.
的长.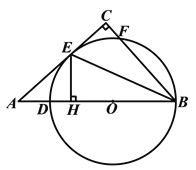
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地走去,y1,y2分别表示小东、小明离B地的距离y(km)与所用时间x(h)的关系,如图所示,根据图象提供的信息,回答下列问题:

(1)试用文字说明交点P所表示的实际意义;
(2)求y1与x的函数关系式;
(3)求A,B两地之间的距离及小明到达A地所需的时间.
相关试题

