【题目】如图1,经过原点O的抛物线![]() (a≠0)与x轴交于另一点A(
(a≠0)与x轴交于另一点A(![]() ,0),在第一象限内与直线y=x交于点B(2,t).
,0),在第一象限内与直线y=x交于点B(2,t).
(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
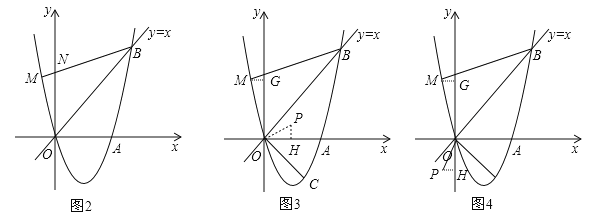
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)C(1,﹣1);(3)存在,P的坐标为(
;(2)C(1,﹣1);(3)存在,P的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
试题分析:(1)由直线解析式可求得B点坐标,由A、B坐标,利用待定系数法可求得抛物线的表达式;
(2)过C作CD∥y轴,交x轴于点E,交OB于点D,过B作BF⊥CD于点F,可设出C点坐标,利用C点坐标可表示出CD的长,从而可表示出△BOC的面积,由条件可得到关于C点坐标的方程,可求得C点坐标;
(3)设MB交y轴于点N,则可证得△ABO≌△NBO,可求得N点坐标,可求得直线BN的解析式,联立直线BM与抛物线解析式可求得M点坐标,过M作MG⊥y轴于点G,由B、C的坐标可求得OB和OC的长,由相似三角形的性质可求得![]() 的值,当点P在第一象限内时,过P作PH⊥x轴于点H,由条件可证得△MOG∽△POH,由
的值,当点P在第一象限内时,过P作PH⊥x轴于点H,由条件可证得△MOG∽△POH,由![]() =
=![]() =
=![]() 的值,可求得PH和OH,可求得P点坐标;当P点在第三象限时,同理可求得P点坐标.
的值,可求得PH和OH,可求得P点坐标;当P点在第三象限时,同理可求得P点坐标.
试题解析:
(1)∵B(2,t)在直线y=x上,∴t=2,∴B(2,2),把A、B两点坐标代入抛物线解析式可得: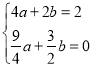 ,解得:
,解得:![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)如图1,过C作CD∥y轴,交x轴于点E,交OB于点D,过B作BF⊥CD于点F,∵点C是抛物线上第四象限的点,∴可设C(t,2t2﹣3t),则E(t,0),D(t,t),∴OE=t,BF=2﹣t,CD=t﹣(2t2﹣3t)=﹣2t2+4t,∴S△OBC=S△CDO+S△CDB=![]() CDOE+
CDOE+![]() CDBF=
CDBF=![]() (﹣2t2+4t)(t+2﹣t)=﹣2t2+4t,∵△OBC的面积为2,∴﹣2t2+4t=2,解得t1=t2=1,∴C(1,﹣1);
(﹣2t2+4t)(t+2﹣t)=﹣2t2+4t,∵△OBC的面积为2,∴﹣2t2+4t=2,解得t1=t2=1,∴C(1,﹣1);

(3)存在.设MB交y轴于点N,如图2,∵B(2,2),∴∠AOB=∠NOB=45°,在△AOB和△NOB中,∵∠AOB=∠NOB,OB=OB,∠ABO=∠NBO,∴△AOB≌△NOB(ASA),∴ON=OA=![]() ,∴N(0,
,∴N(0,![]() ),∴可设直线BN解析式为y=kx+
),∴可设直线BN解析式为y=kx+![]() ,把B点坐标代入可得2=2k+
,把B点坐标代入可得2=2k+![]() ,解得k=
,解得k=![]() ,∴直线BN的解析式为
,∴直线BN的解析式为![]() ,联立直线BN和抛物线解析式可得:
,联立直线BN和抛物线解析式可得: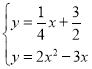 ,解得:
,解得:![]() 或
或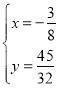 ,∴M(
,∴M(![]() ,
,![]() ),∵C(1,﹣1),∴∠COA=∠AOB=45°,且B(2,2),∴OB=
),∵C(1,﹣1),∴∠COA=∠AOB=45°,且B(2,2),∴OB=![]() ,OC=
,OC=![]() ,∵△POC∽△MOB,∴
,∵△POC∽△MOB,∴![]() =
=![]() =2,∠POC=∠BOM,当点P在第一象限时,如图3,过M作MG⊥y轴于点G,过P作PH⊥x轴于点H,如图3
=2,∠POC=∠BOM,当点P在第一象限时,如图3,过M作MG⊥y轴于点G,过P作PH⊥x轴于点H,如图3
∵∠COA=∠BOG=45°,∴∠MOG=∠POH,且∠PHO=∠MGO,∴△MOG∽△POH,∴![]() =
=![]() =
=![]() =2,∵M(
=2,∵M(![]() ,
,![]() ),∴MG=
),∴MG=![]() ,OG=
,OG=![]() ,∴PH=
,∴PH=![]() MG=
MG=![]() ,OH=
,OH=![]() OG=
OG=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
当点P在第三象限时,如图4,过M作MG⊥y轴于点G,过P作PH⊥y轴于点H,同理可求得PH=![]() MG=
MG=![]() ,OH=
,OH=![]() OG=
OG=![]() ,∴P(﹣
,∴P(﹣![]() ,
,![]() );
);
综上可知:存在满足条件的点P,其坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,AC,PB的延长线相交于点D.
(1)若∠1=20°,求∠APB的度数.
(2)当∠1为多少度时,OP=OD?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10
 km,一艘货轮从B港口沿如图所示的BC方向航行4
km,一艘货轮从B港口沿如图所示的BC方向航行4 km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
A.8
 B.9
B.9 C.6
C.6 D.7
D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
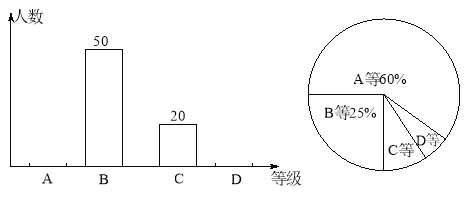
A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,以A为圆心,AB为半径的圆交AD于F,交BC于G,延长BA交圆于E.
(1)若ED与⊙A相切,试判断GD与⊙A的位置关系,并证明你的结论;
(2)在(1)的条件不变的情况下,若GC=CD,求∠C.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,AD是中线,E是AD的中点,过点A作
,AD是中线,E是AD的中点,过点A作 交BE的延长线于F,连接CF.
交BE的延长线于F,连接CF. 求证:
求证: ;
; 如果
如果 ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.
相关试题

