Question

【题目】如图，在平面直角坐标系中，直线l1：y=﹣x与反比例函数y=的图象交于A，B两点（点A在点B左侧），已知A点的纵坐标是2：

（1）求反比例函数的表达式；

（2）将直线l1：y=﹣x向上平移后的直线l2与反比例函数y=在第二象限内交于点C，如果△ABC的面积为30，求平移后的直线l2的函数表达式．

Answer 1

【答案】（1）y= ；（2）y=﹣x+；

【解析】

（1）根据已知条件y=﹣x经过点A，且A点的纵坐标是2，求得点A的坐标，再把点A的坐标代入y=求得k值，即可求得反比例函数的解析式；（2）如图，过F作FD⊥AB于D，过A作AE⊥x轴，则∠FDO=∠OEA=90°，结合A（﹣4，2）可得AE=2，OE=4，AO=2，由此可得AB=2AO=4，根据三角形的面积公式求得DF==3，再证明△AOE∽△OFD，根据相似三角形的性质求得OF=，即可求得点F的坐标，设平移后的直线l2的函数表达式为y=﹣x+b，把点F的坐标代入即可求得b值，从而求得直线l2的函数表达式.

（1）直线l1：y=﹣x经过点A，且A点的纵坐标是2，

∴令y=2，则x=﹣4，

即A（﹣4，2），

∵反比例函数y=的图象经过A点，

∴k=﹣4×2=﹣8，

∴反比例函数的表达式为y=﹣；

（2）如图，过F作FD⊥AB于D，过A作AE⊥x轴，则∠FDO=∠OEA=90°，

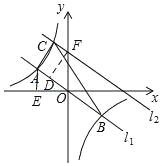
∴AE=2，OE=4，AO=2，

∴AB=2AO=4，

∵直线l1与直线l2平行，△ABC的面积为30，

∴AB×DF=30，即×4×DF=30，

∴DF=3，

∵∠EOF=90°，

∴∠AOE+∠DOF=90°=∠OFD+∠DOF，

∴∠AOE=∠OFD，

∴△AOE∽△OFD，

∴=，即=，

∴FO=，

即F（0，），

设平移后的直线l2的函数表达式为y=﹣x+b，则

=0+b，

∴b=，

∴平移后的直线l2的函数表达式为y=﹣x+．