【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

参考答案:
【答案】(1)结论:FD=FC,DF⊥CF.理由见解析;(2)结论不变.理由见解析;(3)![]() ≤BF
≤BF![]() .
.
【解析】
(1)结论:FD=FC,DF⊥CF.由直角三角形斜边中线定理即可证明;
(2)如图2中,延长AC到M使得CM=CA,延长ED到N,使得DN=DE,连接BN、BM.EM、AN,延长ME交AN于H,交AB于O.想办法证明△ABN≌△MBE,推出AN=EM,再利用三角形中位线定理即可解决问题;
(3)分别求出BF的最大值、最小值即可解决问题;
解:(1)结论:FD=FC,DF⊥CF.
理由:如图1中,
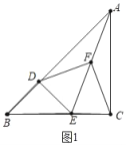
∵∠ADE=∠ACE=90°,AF=FE,
∴DF=AF=EF=CF,
∴∠FAD=∠FDA,∠FAC=∠FCA,
∴∠DFE=∠FDA+∠FAD=2∠FAD,∠EFC=∠FAC+∠FCA=2∠FAC,
∵CA=CB,∠ACB=90°,
∴∠BAC=45°,
∴∠DFC=∠EFD+∠EFC=2(∠FAD+∠FAC)=90°,
∴DF=FC,DF⊥FC.
(2)结论不变.
理由:如图2中,延长AC到M使得CM=CA,延长ED到N,使得DN=DE,连接BN、BM.EM、AN,延长ME交AN于H,交AB于O.
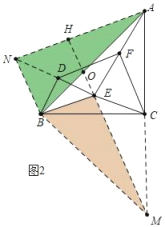
∵BC⊥AM,AC=CM,
∴BA=BM,同法BE=BN,
∵∠ABM=∠EBN=90°,
∴∠NBA=∠EBM,
∴△ABN≌△MBE,
∴AN=EM,∴∠BAN=∠BME,
∵AF=FE,AC=CM,
∴CF=![]() EM,FC∥EM,同法FD=
EM,FC∥EM,同法FD=![]() AN,FD∥AN,
AN,FD∥AN,
∴FD=FC,
∵∠BME+∠BOM=90°,∠BOM=∠AOH,
∴∠BAN+∠AOH=90°,
∴∠AHO=90°,
∴AN⊥MH,FD⊥FC.
(3)![]() .
.
当点![]() 落在
落在![]() 上时,
上时,![]() 取得最大值,
取得最大值,
如图5所示,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() ,
,
∴![]() ,
,
即![]() 的最大值为
的最大值为![]() .
.
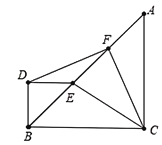
图5
当点![]() 落在
落在![]() 延长线上时,
延长线上时,![]() 取得长最小值,
取得长最小值,
如图6所示,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() ,
,
∴![]() ,
,
即![]() 的最小值为
的最小值为![]() .
.

图6
综上所述,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次
第二次
第三次
第四次
第五次
第六交
甲
9
8
6
7
8
10
乙
8
7
9
7
8
8
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,经过原点O的抛物线
 (a≠0)与x轴交于另一点A(
(a≠0)与x轴交于另一点A( ,0),在第一象限内与直线y=x交于点B(2,t).
,0),在第一象限内与直线y=x交于点B(2,t).(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1:y=﹣
 x与反比例函数y=
x与反比例函数y= 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:(1)求反比例函数的表达式;
(2)将直线l1:y=﹣
 x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y= 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有
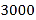 名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.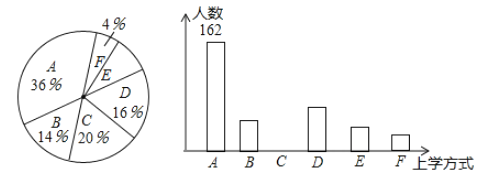
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有_____人,其中选择
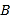 类的人数有_____人;
类的人数有_____人;(2)在扇形统计图中,求
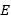 类对应的扇形圆心角
类对应的扇形圆心角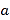 的度数,并补全条形统计图;
的度数,并补全条形统计图;(3)若将
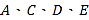 这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC≤BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、点F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 的半径为 4,
的半径为 4,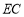 是圆的直径,点
是圆的直径,点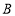 是
是 的切线
的切线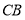 上的一个动点,连接
上的一个动点,连接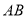 交
交 于点
于点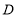 ,弦
,弦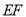 平行于
平行于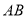 ,连接
,连接 .
. 
(1)试判断直线
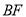 与
与 的位置关系,并说明理由;
的位置关系,并说明理由; (2)当
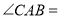 __________时,四边形
__________时,四边形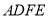 为菱形;
为菱形; (3)当
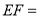 ___________时,四边形
___________时,四边形 为正方形.
为正方形.
相关试题

