【题目】如图,△ABC中,∠ACB=90°,AC≤BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、点F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B=_____.

参考答案:
【答案】45°或30°
【解析】
先确定△CDF是等腰三角形,得出∠CFD=∠CDF=45°,因为不确定△BDE是以那两条边为腰的等腰三角形,故需讨论,①DE=DB,②BD=BE,③DE=BE,然后分别利用角的关系得出答案即可.
∵△CDF中,∠C=90°,且△CDF是等腰三角形,
∴CF=CD,
∴∠CFD=∠CDF=45°,
设∠DAE=x°,由对称性可知,AF=FD,AE=DE,
∴∠FDA=![]() ∠CFD=22.5°,∠DEB=2x°,
∠CFD=22.5°,∠DEB=2x°,
分类如下:
①当DE=DB时,∠B=∠DEB=2x°,
由∠CDE=∠DEB+∠B,得45°+22.5°+x=4x,
解得:x=22.5°.
此时∠B=2x=45°;
见图形(1),说明:图中AD应平分∠CAB.
②当BD=BE时,则∠B=(180°﹣4x)°,
由∠CDE=∠DEB+∠B得:45°+22.5°+x=2x+180°﹣4x,
解得x=37.5°,
此时∠B=(180﹣4x)°=30°.
图形(2)说明:∠CAB=60°,∠CAD=22.5°.
③DE=BE时,则∠B=![]() (180﹣2x)°,
(180﹣2x)°,
由∠CDE=∠DEB+∠B得,45°+22.5°+x=2x+![]() (180﹣2x)°,
(180﹣2x)°,
此方程无解.
∴DE=BE不成立.
综上所述,∠B=45°或30°.
故答案为:45°或30°.
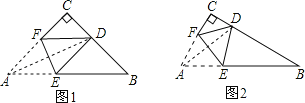
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是线段
是线段 上的任意一点(端点除外),分别以
上的任意一点(端点除外),分别以 ,
, 为斜边并且在
为斜边并且在 的同一侧作等腰直角
的同一侧作等腰直角 和
和 ,连接
,连接 交
交 于点
于点 ,连接
,连接 交
交 于点
于点 ,给出以下三个结论:①
,给出以下三个结论:① ;②
;② ;③
;③ ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:我们知道,比较两数(式)大小有很多方法,“作差法”是常用的方法之一,其原理是不等式(或等式)的性质:若
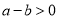 ,则
,则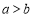 ;若
;若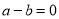 ,则
,则 ;若
;若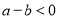 ,则
,则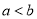 .
.例:已知
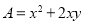 ,
,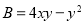 ,其中
,其中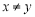 ,求证:
,求证: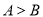 .
.证明:
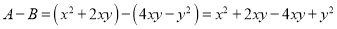
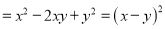 .
.∵
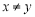 ,∴
,∴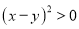 ,∴
,∴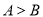 .
.(1)操作感知:比较大小:
①若
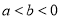 ,则
,则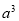 ______
______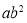 ;
;②
 ______
______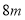 .
.(2)类比探究:已知
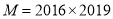 ,
,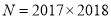 ,试运用上述方法比较
,试运用上述方法比较 、
、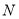 的大小,并说明理由.
的大小,并说明理由.(3)应用拓展:已知
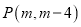 ,
, 为平面直角坐标系中的两点,小明认为,无论
为平面直角坐标系中的两点,小明认为,无论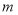 取何值,点
取何值,点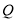 始终在点
始终在点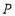 的上方,小明的猜想对吗?为什么?
的上方,小明的猜想对吗?为什么? -
科目: 来源: 题型:
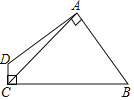
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AD,AC=6,∠DAB=∠DCB=90°,则四边形ABCD的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°.
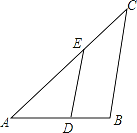
(1)求∠AED和∠ADE的大小;
(2)求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.

(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形
 中,
中, ,
, ,且
,且 ,
, ,对角线
,对角线 .
.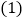 求证:四边形
求证:四边形 是矩形;
是矩形; 如图
如图 ,若动点
,若动点 从点
从点 出发,在
出发,在 边上以每秒
边上以每秒 的速度向点
的速度向点 匀速运动,同时动点
匀速运动,同时动点 从点
从点 出发,在
出发,在 边上以每秒
边上以每秒 的速度向点
的速度向点 匀速运动,运动时间为
匀速运动,运动时间为 秒
秒 ,连接
,连接 、
、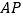 ,若
,若 ,求
,求 的值;
的值; 如图
如图 ,若点
,若点 在对角线
在对角线 上,
上, ,动点
,动点 从
从 点出发,以每秒
点出发,以每秒 的速度沿
的速度沿 运动至点
运动至点 止.设点
止.设点 运动了
运动了 秒,请你探索:从运动开始,经过多少时间,以点
秒,请你探索:从运动开始,经过多少时间,以点 、
、 、
、 为顶点的三角形是等腰三角形?请求出所有可能的结果.
为顶点的三角形是等腰三角形?请求出所有可能的结果.
相关试题

