【题目】在平面直角坐标系中,有三点![]() ,且满足:
,且满足:![]()
(1)求A、B、C三点坐标;
(2)已知,在y轴上有一点![]() ,在坐标轴上是否存在一点P,使△ABP和△ABC的面积相等?若存在,求出P点坐标.若不存在,请说明理由.(C点除外)
,在坐标轴上是否存在一点P,使△ABP和△ABC的面积相等?若存在,求出P点坐标.若不存在,请说明理由.(C点除外)

参考答案:
【答案】(1)![]()
![]()
![]() (2)P(0,5)或P(0,-2)或P(-10,0)
(2)P(0,5)或P(0,-2)或P(-10,0)
【解析】
(1)根据算术平方根的非负性、绝对值的非负性、平方的非负性结合已知条件得出![]() 且
且![]() 且
且![]() ,解出a、b、c的值即可;
,解出a、b、c的值即可;
(2)分①当点P在y轴上时,②当点P在x轴上时两种情况讨论,先求出△ABC的面积,再设出点P的坐标,列出△ABP面积的表达式,进而利用△ABP和△ABC的面积相等得到方程,解方程即可.
解:(1)∵![]() ,且
,且![]() ≥0,
≥0,![]() ≥0,
≥0,![]() ≥0,
≥0,
∴![]() 且
且![]() 且
且![]() ,
,
解得:a=-3,b=3,c=4,
∴A、B、C三点坐标分别为:![]() ,
,![]() ,
,![]() .
.
(2)在坐标轴上存在点P,使△ABP和△ABC的面积相等.理由如下:
如下图1,过点B作BE⊥AC,由第(1)问得:AC=7,BE=3,
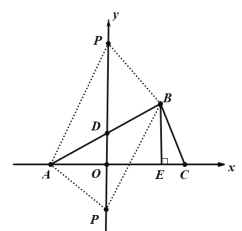
图1
S△ABC=![]() AC·BE=
AC·BE=![]() .
.
①当点P在y轴上时,设点P的坐标为(0,y),
S△ABP=![]() PD·AO+
PD·AO+![]() PD·OE=
PD·OE=![]() PD·(AO+OE) =
PD·(AO+OE) =![]() PD·AE=
PD·AE= ![]() ·|y-
·|y-![]() |×6,
|×6,
∵S△ABP= S△ABC
∴![]() ·|y-
·|y-![]() |×6=
|×6=![]() ,
,
解得:y=5或y=-2,
∴点P的坐标为(0,5)或(0,-2);
②当点P在x轴上时,设点P的坐标为(x,0),如下图2:
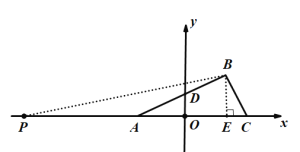
图2
S△ABP=![]() AP·BE=
AP·BE=![]() ·|-3-x|×3,
·|-3-x|×3,
∵S△ABP= S△ABC
∴![]() ·|-3-x|×3=
·|-3-x|×3=![]() ,
,
解得:x=-10或x=4(舍去),
∴点P的坐标为(-10,0).
综上,在坐标轴上存在点P,使△ABP和△ABC的面积相等,点P的坐标为(0,5)或(0,-2)或(-10,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用3辆A型车和2辆B型车载满货物一次可运货17吨;用2辆A型车和3辆B型车载满货物一次可运货l8吨,某物流公刊现有35吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)l辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
-
科目: 来源: 题型:
查看答案和解析>>【题目】据说,我国著名数学家华罗庚在一次访问途中,看到飞机邻座的乘客阅读的杂志上有一道智力题:一个数32768,它是一个正数的立方,希望求它的立方根,华罗庚不假思索给出了答案,邻座乘客非常惊奇,很想得知其中的奥秘,你知道华罗庚是怎样准确计算出的吗?请按照下面的问题试一试:
(1)由
 ,因为
,因为 ,请确定
,请确定 是______位数;
是______位数;(2)由32768的个位上的数是8,请确定
 的个位上的数是________,划去32768后面的三位数768得到32,因为
的个位上的数是________,划去32768后面的三位数768得到32,因为 ,请确定
,请确定 的十位上的数是_____________;
的十位上的数是_____________;(3)已知
 和
和 分别是两个数的立方,仿照上面的计算过程,请计算:
分别是两个数的立方,仿照上面的计算过程,请计算: ;
;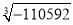 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=
 的图象经过A,B两点,则菱形ABCD的面积为( )
的图象经过A,B两点,则菱形ABCD的面积为( )
A.2
B.4
C.2
D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, 分别是
分别是 上的点,作
上的点,作 ,垂足分别是
,垂足分别是 若
若 , 下面三个结论:①
, 下面三个结论:① ②
② ③
③ 其中正确的是( )
其中正确的是( )
A.①③B.②③C.①②D.①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
①c>0;
②若点B(﹣ ,y1)、C(﹣
,y1)、C(﹣  ,y2)为函数图象上的两点,则y1<y2;
,y2)为函数图象上的两点,则y1<y2;
③2a﹣b=0;
④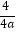 <0,
<0,
其中,正确结论的个数是( )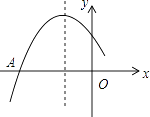
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(x,y)的坐标满足

(1)求点P的坐标.(用含m,n的式子表示x,y)
(2)如果点P在第二象限,且符合要求的整数只有两个,求n的范围.
(3)如果点P在第二象限,且所有符合要求的整数m之和为9,求n的范围.
相关试题

