【题目】已知:用3辆A型车和2辆B型车载满货物一次可运货17吨;用2辆A型车和3辆B型车载满货物一次可运货l8吨,某物流公刊现有35吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)l辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
参考答案:
【答案】(1)1辆A型车辆装满货物一次可运3吨,1辆B型车装满货物一次可运4吨.(2)有3种租车方案:方案一:A型车9辆,B型车2辆;方案二:A型车5辆,B型车5辆;方案三:A型车1辆,B型车8辆.
【解析】
(1)根据“用3辆A型车和2辆B型车载满货物一次可运货17吨”“用2辆A型车和3辆B型车载满货物一次可运货18吨”,分别得出等式方程,组成方程组求出即可;
(2)由题意理解出:3a+4b=35,解此二元一次方程,求出其整数解,得到三种租车方案.
(1)设每辆A型车、B型车都装满货物一次可以分别运货x吨、y吨,
由题意列方程组为:![]()
解得![]()
答:1辆A型车辆装满货物一次可运3吨,1辆B型车装满货物一次可运4吨.
(2)由题意得:3a+4b=35
∵a、b都是整数
∴![]() 或
或![]() 或
或![]()
答:有3种租车方案:
方案一:A型车9辆,B型车2辆;
方案二:A型车5辆,B型车5辆;
方案三:A型车1辆,B型车8辆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
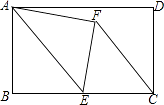
A.
B.
C.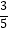
D.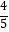
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形
 的底边
的底边 长为
长为 ,面积是
,面积是 , 腰
, 腰 的垂直平分线
的垂直平分线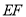 分别交
分别交 边于
边于 点.若点
点.若点 为
为 边的中点,点
边的中点,点 为线段EF上一动点,则
为线段EF上一动点,则 周长的最小值为( )
周长的最小值为( )
A.
 B.
B. C.
C.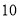 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按图中所标注的数据,计算图中实线所围成的面积S是( )

A.50B.62C.65D.68
-
科目: 来源: 题型:
查看答案和解析>>【题目】据说,我国著名数学家华罗庚在一次访问途中,看到飞机邻座的乘客阅读的杂志上有一道智力题:一个数32768,它是一个正数的立方,希望求它的立方根,华罗庚不假思索给出了答案,邻座乘客非常惊奇,很想得知其中的奥秘,你知道华罗庚是怎样准确计算出的吗?请按照下面的问题试一试:
(1)由
 ,因为
,因为 ,请确定
,请确定 是______位数;
是______位数;(2)由32768的个位上的数是8,请确定
 的个位上的数是________,划去32768后面的三位数768得到32,因为
的个位上的数是________,划去32768后面的三位数768得到32,因为 ,请确定
,请确定 的十位上的数是_____________;
的十位上的数是_____________;(3)已知
 和
和 分别是两个数的立方,仿照上面的计算过程,请计算:
分别是两个数的立方,仿照上面的计算过程,请计算: ;
;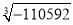 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=
 的图象经过A,B两点,则菱形ABCD的面积为( )
的图象经过A,B两点,则菱形ABCD的面积为( )
A.2
B.4
C.2
D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,有三点
 ,且满足:
,且满足:
(1)求A、B、C三点坐标;
(2)已知,在y轴上有一点
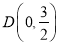 ,在坐标轴上是否存在一点P,使△ABP和△ABC的面积相等?若存在,求出P点坐标.若不存在,请说明理由.(C点除外)
,在坐标轴上是否存在一点P,使△ABP和△ABC的面积相等?若存在,求出P点坐标.若不存在,请说明理由.(C点除外)
相关试题

