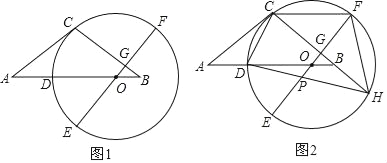
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是![]() 的中点.
的中点.
(1)求证:AC是⊙O的切线;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
(3)在(2)的条件下,连接CD,若tan∠HDC=![]() ,CG=4,求OP的长.
,CG=4,求OP的长.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析: ![]() 连接OC.
连接OC. ![]() 得到
得到![]()
![]()
![]() 得出
得出![]() 即可证明AC是
即可证明AC是![]() 的切线.
的切线.
![]() 如图2中,连接OC,首先证明
如图2中,连接OC,首先证明![]() 再证明点P在以F为圆心FC为半径的圆上,即可解决问题;
再证明点P在以F为圆心FC为半径的圆上,即可解决问题;
![]() 在
在![]() 中,利用
中,利用![]() 求出
求出![]() 根据勾股定理求得
根据勾股定理求得![]()
![]() 在Rt
在Rt ![]() 中,根据勾股定理得,
中,根据勾股定理得, ![]() 利用
利用![]() 中的结论即可求出
中的结论即可求出![]() 的长度.
的长度.
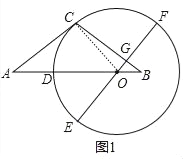
试题解析:(1)证明:如图1中,连接OC.
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵点D是![]() 的中点,
的中点,
∴![]() =
=![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
∴AC是![]() 的切线,
的切线,
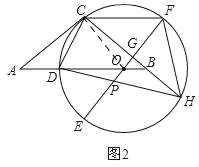
(2)证明:如图2中,连接OC,
∵![]()
∴![]()
∴EF垂直平分HC,
∴![]()
∵![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴点P在以F为圆心FC为半径的圆上,
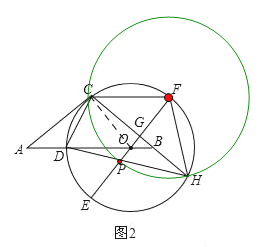
∴![]()
∵![]()
∴![]()
即![]()
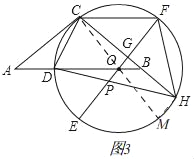
(3)如图3,连接CO并延长交![]() 于M,连接
于M,连接![]() ,
,
∴![]()
∵![]() 于G,
于G,
![]()
在![]() 中,
中, ![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴OG∥MH,
∵![]()
∴![]()
∴![]()
在Rt ![]() 中,根据勾股定理得,
中,根据勾股定理得, ![]()
由(2)知, ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)36+(-25)+12+(-15);
(2) 9+(-2.5)+(+6)+(-3.5);
(3)3.7+(-9.1)+6.3+(-0.9) ;
(4)10-(-5)-(-6)-(+18)
(5)(-12)-6-(-8)-(-12);
(6)5-(-5)+(-10)+0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y=
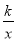 (x>0)的图象过点A.
(x>0)的图象过点A.(1)求直线l和反比例函数的解析式;
(2)在函数y=
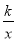 (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.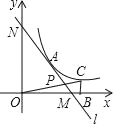
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=mx与双曲线y=
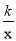 交于A、B两点,D为x轴上一点,连接BD交y轴与点C,若C(0,-2)恰好为BD中点,且△ABD的面积为6,则B点坐标为__________.
交于A、B两点,D为x轴上一点,连接BD交y轴与点C,若C(0,-2)恰好为BD中点,且△ABD的面积为6,则B点坐标为__________.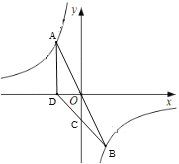
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD分别沿AE、CF折叠,若B、D两点恰好都落在对角线的交点O上,下列说法:①四边形AECF为菱形,②∠AEC=120°,③若AB=2,则四边形AECF的面积为
 ,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)
,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD的边长是4,∠DAB=60,点M,N分别在边AD,AB上,MN⊥AC,垂足为P,把△AMN沿MN折叠得到△A'MN,若△A'DC恰为等腰三角形,则AP的长为_____。

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式写出省略加号的和的形式,并说出它们的两种读法:
(1)(-20)-(+10)+(-5)-(-6);
(2)(+8.5)-(-2.9)-2.5+(-5.3).
相关试题

