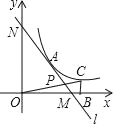
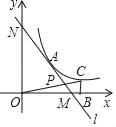
【题目】如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y=![]() (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l和反比例函数的解析式;
(2)在函数y=![]() (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
参考答案:
【答案】(1)y=﹣![]() x+4,y=
x+4,y=![]() ;(2)点P的坐标为(
;(2)点P的坐标为(![]() ,1).
,1).
【解析】试题分析:(1)设直线l的解析式为![]() ,利用待定系数法即可求得直线的解析式;根据已知求得A点的坐标,然后把A代入
,利用待定系数法即可求得直线的解析式;根据已知求得A点的坐标,然后把A代入![]() 即可求得解析式;
即可求得解析式;
(2)根据反比例函数系数k的几何意义得出![]() 进而得出
进而得出![]() 设P点的坐标为
设P点的坐标为![]() 根据
根据![]() 即可求得
即可求得![]() 的值,进而求得P的坐标.
的值,进而求得P的坐标.
试题解析:(1)设直线l的解析式为![]() ,
,
将![]() 代入
代入![]()
得![]() 解得:
解得:  ,
,
∴直线l的解析式为![]()
∵点A为线段MN的中点,
∴点A的坐标为![]()
将![]() 代入
代入![]()
得![]()
∴反比例函数解析式为![]()
(2)∵![]()
∴![]()
∵点![]()
∴![]()
设点P的坐标为![]() 则
则![]()
∴![]()
∴![]()
则![]()
∴点P的坐标为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:点A、B在数轴上分别表示有理数a、b,
 表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①,
表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①, ;
;当A、B两点都在原点右侧时,如图②,
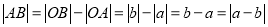 ;
;当AB两点都在原点左侧时,如图③,
 ;
;当AB两点在原点两侧时,如图④,
 ;
;
请根据上述结论,回答下列问题:
(1)数轴上表示2和5的两点问距离是______,数轴上表示2和-6的两点间距高是_________,数轴上表示-1和3的两点间距离是____________.
(2)数轴上表示x和-1的两点A和B之间的距离可表示为_________,若|AB|=2,则x的值为_____________.
(3)当
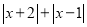 取最小值时,请写出所有符合条件的x的整数值_______________.
取最小值时,请写出所有符合条件的x的整数值_______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明到青城山游玩,乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200 m,缆车行驶的路线与水平夹角∠α=16°,当缆车继续由点B到达点D时,它又走过了200 m,缆车由点B到点D的行驶路线与水平夹角∠β=42°,求缆车从点A到点D垂直上升的距离.(结果保留整数)(参考数据:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)36+(-25)+12+(-15);
(2) 9+(-2.5)+(+6)+(-3.5);
(3)3.7+(-9.1)+6.3+(-0.9) ;
(4)10-(-5)-(-6)-(+18)
(5)(-12)-6-(-8)-(-12);
(6)5-(-5)+(-10)+0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=mx与双曲线y=
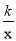 交于A、B两点,D为x轴上一点,连接BD交y轴与点C,若C(0,-2)恰好为BD中点,且△ABD的面积为6,则B点坐标为__________.
交于A、B两点,D为x轴上一点,连接BD交y轴与点C,若C(0,-2)恰好为BD中点,且△ABD的面积为6,则B点坐标为__________.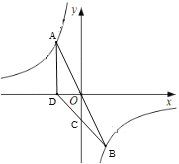
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是
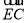 的中点.
的中点.(1)求证:AC是⊙O的切线;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
(3)在(2)的条件下,连接CD,若tan∠HDC=
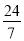 ,CG=4,求OP的长.
,CG=4,求OP的长.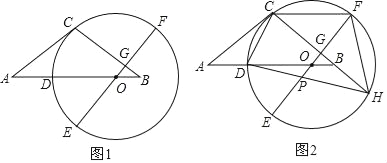
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD分别沿AE、CF折叠,若B、D两点恰好都落在对角线的交点O上,下列说法:①四边形AECF为菱形,②∠AEC=120°,③若AB=2,则四边形AECF的面积为
 ,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)
,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)
相关试题

