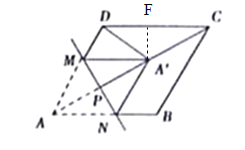
【题目】菱形ABCD的边长是4,∠DAB=60,点M,N分别在边AD,AB上,MN⊥AC,垂足为P,把△AMN沿MN折叠得到△A'MN,若△A'DC恰为等腰三角形,则AP的长为_____。

参考答案:
【答案】![]() ,
, ![]()
【解析】解:设AP=x,则A′P=AP=x.∵菱形ABCD的边长是4,∠DAB=60,∴菱形较短的对角线为4,较长的对角线AC=![]() ,∴A′C=
,∴A′C=![]() .∵△A'DC为等腰三角形,∴分三种情况讨论:
.∵△A'DC为等腰三角形,∴分三种情况讨论:
①A′C=DC,即![]() =4,解得:x=
=4,解得:x=![]() ;
;
②DC=DA′.∵DC=4,∴DA′=4,此时A′与A重合,此种情况不成立;
③DA′=CA′=![]() .∵ABCD是菱形,∠DAB=60,∴∠DCA=30°,过A′作A′F⊥DC于F.∵DA′=CA′,∴DF=FC=2,∴A′F=
.∵ABCD是菱形,∠DAB=60,∴∠DCA=30°,过A′作A′F⊥DC于F.∵DA′=CA′,∴DF=FC=2,∴A′F=![]() ,∴A′C=2 A′F=
,∴A′C=2 A′F=![]() ,
,
∴![]() =
=![]() ,解得:x=
,解得:x=![]() .
.
综上所述:AP的长为![]() 或
或![]() .
.
故答案为: ![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=mx与双曲线y=
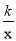 交于A、B两点,D为x轴上一点,连接BD交y轴与点C,若C(0,-2)恰好为BD中点,且△ABD的面积为6,则B点坐标为__________.
交于A、B两点,D为x轴上一点,连接BD交y轴与点C,若C(0,-2)恰好为BD中点,且△ABD的面积为6,则B点坐标为__________.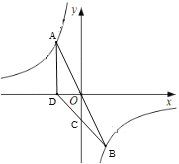
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是
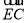 的中点.
的中点.(1)求证:AC是⊙O的切线;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
(3)在(2)的条件下,连接CD,若tan∠HDC=
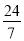 ,CG=4,求OP的长.
,CG=4,求OP的长.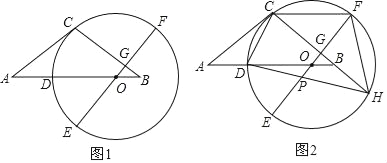
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD分别沿AE、CF折叠,若B、D两点恰好都落在对角线的交点O上,下列说法:①四边形AECF为菱形,②∠AEC=120°,③若AB=2,则四边形AECF的面积为
 ,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)
,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式写出省略加号的和的形式,并说出它们的两种读法:
(1)(-20)-(+10)+(-5)-(-6);
(2)(+8.5)-(-2.9)-2.5+(-5.3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P、Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.(顶点都在格点上的四边形称为格点四边形)
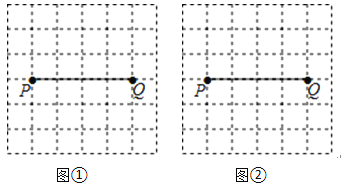
(1)在图①中画出一个面积最小的中心对称图形PAQB,
(2)在图②中画出一个四边形PCQD,使其是轴对称图形但不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年3月,某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(x均为整数,总分100分),绘制了如下尚不完整的统计图表.
调查结果统计表
组别
成绩分组(单位:分)
频数
频率
A
80≤x<85
50
0.1
B
85≤x<90
75
C
90≤x<95
150
c
D
95≤x≤100
a
合计
b
1
根据以上信息解答下列问题:
(1)统计表中,a=_____,b=_____,c=_____;
(2)扇形统计图中,m的值为_____,“C”所对应的圆心角的度数是_____;
(3)若参加本次竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?

相关试题

