【题目】如图,将矩形纸片ABCD分别沿AE、CF折叠,若B、D两点恰好都落在对角线的交点O上,下列说法:①四边形AECF为菱形,②∠AEC=120°,③若AB=2,则四边形AECF的面积为![]() ,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)
,④AB:BC=1:2,其中正确的说法有_____.(只填写序号)

参考答案:
【答案】①②③
【解析】
根据折叠性质可得OC=CD=AB=OA,∠COF=∠EOA=∠B=∠D=90°,∠OCF=∠DCF,∠BAE=∠OAE,即可得出∠ACB=30°,进而可得∠OCF=∠DCF=∠BAE=∠OAE=30°,可证明
AE//CF,AE=CE,根据矩形性质可得CE//AF,即可得四边形AECF是平行四边形,进而可得四边形AECF为菱形,由∠BAE=30°,可得∠AEB=60°,即可得∠AEC=120°,根据含30°角的直角三角形的性质可求出BE的长,即可得OE的长,根据菱形的面积公式即可求出四边形AECF的面积,根据含30°角的直角三角形的性质即可求出AB:BC的值,综上即可得答案.
∵矩形ABCD分别沿AE、CF折叠,B、D两点恰好都落在对角线的交点O上,
∴OC=CD=AB=OA,∠COF=∠EOA=∠B=∠D=90°,∠OCF=∠DCF,∠BAE=∠OAE,
∴∠ACB=∠CAD=30°,∠BAC=∠ACD=60°,
∵∠OCF=∠DCF,∠BAE=∠OAE,
∴∠OCF=∠DCF=∠BAE=∠OAE=30°,
∴AE//CF,AE=CE,
∴四边形AECF是平行四边形,
∵AE=CE,
∴四边形AECF是菱形,故①正确,
∵∠BAE=30°,∠B=90°,
∴∠AEB=60°,
∴∠AEC=120°,故②正确,
设BE=x,
∵∠BAE=30°,
∴AE=2x,
∴x2+22=(2x)2,
解得:x=![]() ,
,
∴OE=BE=![]() ,
,
∴S菱形AECF=![]() EF
EF![]() AC=
AC=![]() ×
×![]() ×4=
×4=![]() ,故③正确,
,故③正确,
∵∠ACB=30°,
∴AC=2AB,
∴BC=![]() =
=![]() AB,
AB,
∴AB:BC=1:![]() ,故④错误,
,故④错误,
综上所述:正确的结论有①②③,
故答案为:①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y=
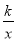 (x>0)的图象过点A.
(x>0)的图象过点A.(1)求直线l和反比例函数的解析式;
(2)在函数y=
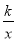 (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.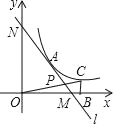
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=mx与双曲线y=
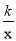 交于A、B两点,D为x轴上一点,连接BD交y轴与点C,若C(0,-2)恰好为BD中点,且△ABD的面积为6,则B点坐标为__________.
交于A、B两点,D为x轴上一点,连接BD交y轴与点C,若C(0,-2)恰好为BD中点,且△ABD的面积为6,则B点坐标为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是
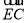 的中点.
的中点.(1)求证:AC是⊙O的切线;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
(3)在(2)的条件下,连接CD,若tan∠HDC=
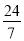 ,CG=4,求OP的长.
,CG=4,求OP的长.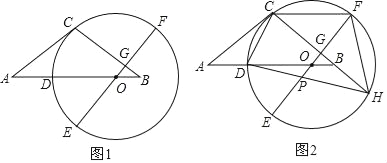
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD的边长是4,∠DAB=60,点M,N分别在边AD,AB上,MN⊥AC,垂足为P,把△AMN沿MN折叠得到△A'MN,若△A'DC恰为等腰三角形,则AP的长为_____。

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式写出省略加号的和的形式,并说出它们的两种读法:
(1)(-20)-(+10)+(-5)-(-6);
(2)(+8.5)-(-2.9)-2.5+(-5.3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P、Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.(顶点都在格点上的四边形称为格点四边形)
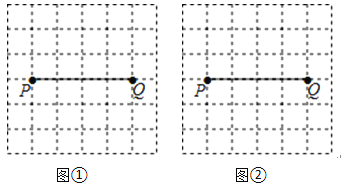
(1)在图①中画出一个面积最小的中心对称图形PAQB,
(2)在图②中画出一个四边形PCQD,使其是轴对称图形但不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.
相关试题

