搜索
【题目】阅读：所谓勾股数就是满足方程x2+y2=z2的正整数解，即满足勾股定理的三个正整数构成的一组数．我国古代数学专著《九章算术》一书，在世界上第一次给出该方程的解为：
，y=mn，
，其中m>n>0，m、n是互质的奇数．应用：当n=5时，求一边长为12的直角三角形另两边的长．
参考答案：
【答案】见解析
【解析】分析：由n=5，得到
①，y=5m②，
③，根据直角三角形有一边长为12，列方程即可得到结论．
详解：∵n=5，直角三角形一边长为12，
∴有三种情况：
当x =12 时，
.
解得m1=7，m2= -7（舍去）.
∴y= mn =35.
∴
.
∴该情况符合题意.
② 当y =12时，
5m =12,
.
∵m为奇数，
∴舍去.
③ 当z =12时，
，
，
此方程无实数解.
综上所述：当n=5时, 一边长为12的直角三角形另两边的长分别为35，37.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：有理数m所表示的点到表示3的点距离4个单位，a、b互为相反数，且都不为零，c、d互为倒数.
（1）求m的值，
（2）求：
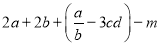的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，池塘边有一块长为18米，宽为10米的长方形土地，现在将其余三面留出宽都是x米的小路，中间余下的长方形部分做菜地，用代数式表示：
(1)菜地的长a=___米，宽b=___米；
(2)菜地的面积S=___平方米；
(3)求当x=1米时，菜地的面积。
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了迎接“六一”国际儿童节，某童装品牌专卖店准备购进甲、乙两种童装，这两种童装的进价和售价如下表：
价格
甲
乙
进价（元/件）
m
m+20
售价（元/件）
150
160
如果用5000元购进甲种童装的数量与用6000元购进乙种童装的数量相同．
（1）求m的值；
（2）要使购进的甲、乙两种童装共200件的总利润（利润＝售价﹣进价）不少于8980元，且甲种童装少于100件，问该专卖店有哪几种进货方案？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校为了解全校学生下学期参加社区活动的情况，学校随机调查了本校50名学生参加社区活动的次数，并将调查所得的数据整理如下：
活动次数x
频数
频率
0<x≤3
10
0.20
3<x≤6
a
0.24
6<x≤9
16
0.32
9<x≤12
m
b
12<x≤15
4
0.08
15<x≤18
2
n
根据以上图表信息，解答下列问题：
（1）表中a=___，b=___；
（2）请把频数分布直方图补充完整（画图后请标注相应的数据）；
（3）若该校共有1500名学生，请估计该校在下学期参加社区活动超过6次的学生有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
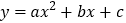(a、b、c是常数，
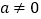)的对称轴为直线
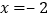．(1) b=______；(用含a的代数式表示)
(2)当
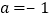时，若关于x的方程
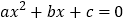在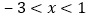
的范围内有解，求c的取值范围；(3)若抛物线过点(
，)，当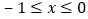
时，抛物线上的点到x轴距离的最大值为4，求a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AD∥BC，AD＝12cm，BC＝15cm，∠B＝90°，DC＝5cm．点P从点A向点D以lcm/s的速度运动，到D点停止，点Q从点C向B点以2cm/s的速度运动，到B点停止，点P，Q同时出发，设运动时间为t（s）．
（1）用含t的代数式表示：AP＝ ；BQ＝ ．
（2）当t为何值时，四边形PDCQ是平行四边形？
（3）当t为何值时，△QCD是直角三角形？
相关试题
