【题目】为了迎接“六一”国际儿童节,某童装品牌专卖店准备购进甲、乙两种童装,这两种童装的进价和售价如下表:
价格 | 甲 | 乙 |
进价(元/件) | m | m+20 |
售价(元/件) | 150 | 160 |
如果用5000元购进甲种童装的数量与用6000元购进乙种童装的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种童装共200件的总利润(利润=售价﹣进价)不少于8980元,且甲种童装少于100件,问该专卖店有哪几种进货方案?
参考答案:
【答案】(1)m=100(2)两种方案
【解析】
(1)用总价除以单价表示出购进童装的数量,根据两种童装的数量相等列出方程求解即可;
(2)设购进甲种童装x件,表示出乙种童装(200-x)件,然后根据总利润列出一元一次不等式,求出不等式组的解集后,再根据童装的件数是正整数解答;设总利润为W,表示出利润,求得最值即可.
(1)根据题意可得:![]() ,
,
解得:m=100,
经检验m=100是原方程的解;
(2)设甲种童装为x件,可得:![]() ,
,
解得:98≤x<100,
因为x取整数,
所以有两种方案:
方案一:甲98,乙102;
方案二:甲99,乙101;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为m的正三角形,D,E,F分别在边AB,BC,CA上,AE,BF交于点P,BF,CD交于点Q,CD,AE交于点R,若
 =
=  =
=  =k(0<k<
=k(0<k<  ).
).
(1)求∠PQR的度数;
(2)求证:△ARD∽△ABE;
(3)求△PQR与△ABC的面积之比(用含k的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.
(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:CO平分∠BOD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】1949年9月27日,全国政协第一届全体会议上通过的《关于中华人民共和国国都、纪年、国歌、国徽、国旗的决议》中,第四点规定:“中华人民共和国的国旗为红底五星旗(如图1),象征中国革命人民大团结.长宽比例为3:2,左上方缀黄色五角星五颗,四颗小星环拱在一颗大星的右面,并各有一个角尖正对大星的中心点.”

第31届夏季奥林匹克运动会于2016年8月5日﹣21日在巴西的里约热内卢举行.在此次的奥运颁奖舞台上出了尴尬情况,多名细心网友指出,射击和游泳颁奖仪式中,冉冉升起的五星红旗被搞错了(如图2).
请你先阅读五星红旗制作的相关规定,再仔细观察图①和图②中的国旗,用所学到的图形知识和语言解释错误的原因.
错误的原因是:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
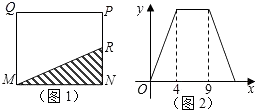
A.当x=2时,y=5
B.矩形MNPQ的面积是20
C.当x=6时,y=10
D.当y= 时,x=3
时,x=3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在解方程
 x+
x+ (x﹣94)=35时,小明被难住.以下是小明、小丽、小飞同学的对话和解答过程,请你将其补充完整:
(x﹣94)=35时,小明被难住.以下是小明、小丽、小飞同学的对话和解答过程,请你将其补充完整:小明:你俩只要帮我讲讲解此方程第一步的想法、依据就可以了.
小丽:解此方程的第一步,我观察到含有括号,我认为应先_____,依据是_____,就可以考虑合并同类项了.
小明利用小丽的想法写出了完整的解答过程如下:
小飞:解此方程的第一步还可以这样想,我观察到此方程含分母,我认为应先_____,在方程两边都_____,依据是_____.
小明利用小飞的想法写出了完整的解答过程如下:
相关试题

