【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
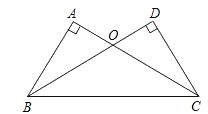
(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)利用“HL”证明Rt△ABC和Rt△DCB全等,根据全等三角形对应边相等可得AB=DC,然后利用“角角边”证明△ABO和△DCO全等即可;
(2)根据全等三角形对应边相等可得AO=DO,然后求出OB=OC,再根据等腰三角形的定义解答.
试题解析:(1)在Rt△ABC和Rt△DCB中,
![]() ,
,
∴Rt△ABC≌Rt△DCB(HL),
∴AB=DC,
在△ABO和△DCO中,
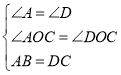 ,
,
∴△ABO≌△DCO(AAS);
(2)△OBC是等腰三角形.
理由如下:∵△ABO≌△DCO,
∴AO=DO,
∵AC=BD,
∴AC-AO=BD-DO,
即OB=OC,
∴△OBC是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=
 ,求AB的长。
,求AB的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,BC=5
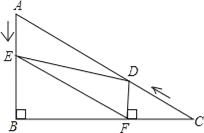
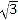 ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.(1)AC的长是 ,AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)当t为何值,△BEF的面积是2
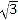 ?
?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一种新型娱乐设施的示意图,x轴所在位置记为地面,平台AB∥x轴,OA=6米,AB=2米,BC是反比例函数y=
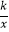 的图象的一部分,CD是二次函数y=﹣x2+mx+n图象的一部分,连接点C为抛物线的顶点,且C点到地面的距离为2米,D点是娱乐设施与地面的一个接触点.
的图象的一部分,CD是二次函数y=﹣x2+mx+n图象的一部分,连接点C为抛物线的顶点,且C点到地面的距离为2米,D点是娱乐设施与地面的一个接触点. 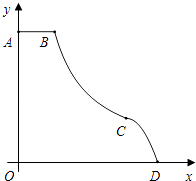
(1)试求k,m,n的值;
(2)试求点B与点D的水平距离. -
科目: 来源: 题型:
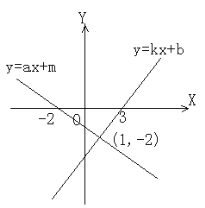
查看答案和解析>>【题目】函数y=kx+b和函数y=ax+m的图像如图所示,求下列不等式(组)的解集
(1) kx+b <ax+m的解集是
(2)
 的解集是
的解集是 (3)
 的解集是
的解集是 (4)
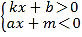 的解集是
的解集是 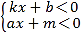
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD与正方形AEFG的边AB,AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE,DG.
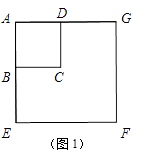
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;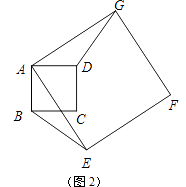
(2)如图3,如果α=45°,AB=2,AE=3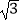 .
.
①求BE的长;②求点A到BE的距离;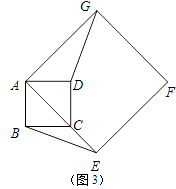
(3)当点C落在直线BE上时,连接FC,直接写出∠FCD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.
如图,抛物线y=x2﹣2x﹣3与x轴交于点A,B,与y轴交于点D,以AB为直径,在x轴上方作半圆交y轴于点C,半圆的圆心记为M,此时这个半圆与这条抛物线x轴下方部分组成的图形就称为“蛋圆”.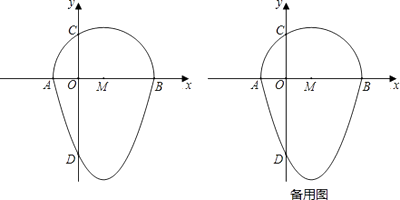
(1)直接写出点A,B,C的坐标及“蛋圆”弦CD的长;
A , B , C , CD=;
(2)如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.
①求经过点C的“蛋圆”切线的解析式;
②求经过点D的“蛋圆”切线的解析式;
(3)由(2)求得过点D的“蛋圆”切线与x轴交点记为E,点F是“蛋圆”上一动点,试问是否存在S△CDE=S△CDF , 若存在请求出点F的坐标;若不存在,请说明理由;
(4)点P是“蛋圆”外一点,且满足∠BPC=60°,当BP最大时,请直接写出点P的坐标.
相关试题

