【题目】定义:把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.
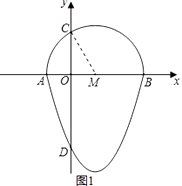
如图,抛物线y=x2﹣2x﹣3与x轴交于点A,B,与y轴交于点D,以AB为直径,在x轴上方作半圆交y轴于点C,半圆的圆心记为M,此时这个半圆与这条抛物线x轴下方部分组成的图形就称为“蛋圆”.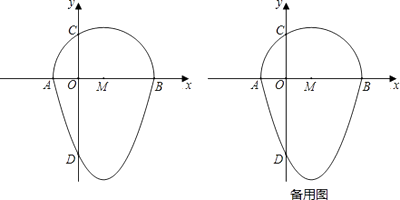
(1)直接写出点A,B,C的坐标及“蛋圆”弦CD的长;
A , B , C , CD=;
(2)如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.
①求经过点C的“蛋圆”切线的解析式;
②求经过点D的“蛋圆”切线的解析式;
(3)由(2)求得过点D的“蛋圆”切线与x轴交点记为E,点F是“蛋圆”上一动点,试问是否存在S△CDE=S△CDF , 若存在请求出点F的坐标;若不存在,请说明理由;
(4)点P是“蛋圆”外一点,且满足∠BPC=60°,当BP最大时,请直接写出点P的坐标.
参考答案:
【答案】
(1)(﹣1,0);(3,0);(0, ![]() );3+
);3+ ![]()
(2)解:①如图2,NC⊥CM,可求得N(﹣3,0),
∴经过点C的“蛋圆”切线的解析式为: ![]() ,
,
②过点D的“蛋圆”切线的解析式为:y=kx﹣3,
由 ![]() ,
,
得:x2﹣(2+k)x=0,
∵直线与抛物线只有一个交点,
∴k=﹣2,
∴经过点D的“蛋圆”切线的解析式为:y=﹣2x﹣3
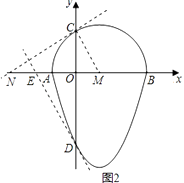
(3)解:如图3,∵经过点D的“蛋圆”切线的解析式为:y=﹣2x﹣3,
∴E点坐标为( ![]() ,0),
,0),
∵S△CDE=S△CDF,
∴F点的横坐标为 ![]() ,
,
在Rt△MQF1中可求得F′Q= ![]() ,
,
把x= ![]() 代入y=x2﹣2x﹣3,可求得y=
代入y=x2﹣2x﹣3,可求得y= ![]() .
.
∴F′( ![]() ,
, ![]() ),F′′(
),F′′( ![]() ,
, ![]() )
)
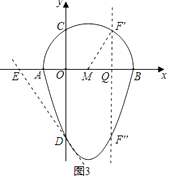
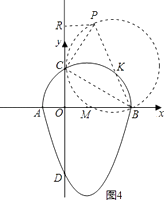
(4)解:如图4,∵∠BPC=60°保持不变,
因此点P在一圆弧上运动.
此圆是以K为圆心(K在BC的垂直平分线上,且∠BKC=120°),BK为半径.
当BP为直径时,BP最大.
在Rt△PCR中可求得PR=1,RC= ![]() .
.
所以点P的坐标为(1,2 ![]() ).
).
【解析】解:(1)当y=0时,x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,
当x=0时,y=3,
∴A(﹣1,0),B(3,0),OD=3,
如图1,连接MC,由题意得,OM=1,MC=2,
∴OC= ![]() =
= ![]() ,
,
∴C(0, ![]() ),CD=3+
),CD=3+ ![]() ,
,
所以答案是:(﹣1,0);(3,0);(0, ![]() );3+
);3+ ![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
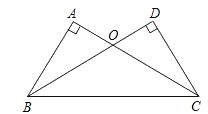
(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.
-
科目: 来源: 题型:
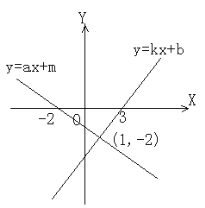
查看答案和解析>>【题目】函数y=kx+b和函数y=ax+m的图像如图所示,求下列不等式(组)的解集
(1) kx+b <ax+m的解集是
(2)
 的解集是
的解集是 (3)
 的解集是
的解集是 (4)
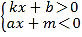 的解集是
的解集是 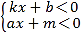
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD与正方形AEFG的边AB,AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE,DG.
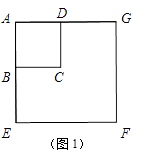
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;
(2)如图3,如果α=45°,AB=2,AE=3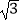 .
.
①求BE的长;②求点A到BE的距离;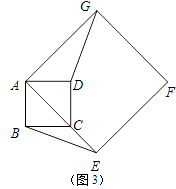
(3)当点C落在直线BE上时,连接FC,直接写出∠FCD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列单项式:
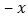 ,
,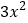 ,
,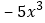 ,
,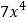 ,…
,…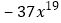 ,
,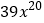 ,…写出第
,…写出第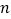 个单项式,为了解这个问题,特提供下面的解题思路.
个单项式,为了解这个问题,特提供下面的解题思路. 这组单项式的系数的符号,绝对值规律是什么?
这组单项式的系数的符号,绝对值规律是什么? 这组单项式的次数的规律是什么?
这组单项式的次数的规律是什么? 根据上面的归纳,你可以猜想出第
根据上面的归纳,你可以猜想出第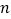 个单项式是什么?
个单项式是什么?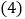 请你根据猜想,请写出第
请你根据猜想,请写出第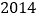 个,第
个,第 个单项式.
个单项式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在Rt ΔABC中,∠ABC=900, AB=BC=2.
(1)用尺规作∠A的平分线AD.
(2)角平分线AD交BC于点D,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
(2)植树节期间,两所学校共植树834棵,其中海石中学植树的数量比励东中学的2倍少3棵,两校各植树多少棵?
相关试题

