【题目】在平面直角坐标系中,已知平行四边形ABCD的点A(0,﹣2)、点B(3m,4m+1)(m≠﹣1),点C(6,2),则对角线BD的最小值是__.
参考答案:
【答案】6
【解析】如图,
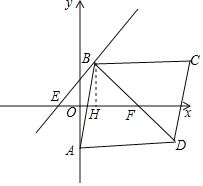
∵点B(3m,4m+1),
∴令![]() ,
,
∴y=![]() x+1,
x+1,
∴B在直线y=![]() x+1上,
x+1上,
∴当BD⊥直线y=![]() x+1时,BD最小,
x+1时,BD最小,
过B作BH⊥x轴于H,则BH=4m+1,
∵BE在直线y=![]() x+1上,且点E在x轴上,
x+1上,且点E在x轴上,
∴E(![]() ,0),G(0,1)
,0),G(0,1)
∵F是AC的中点,
∵A(0,2),点C(6,2),
∴F(3,0)
在Rt△BEF中,
∵BH2=EHFH,
∴(4m+1)2=(3m+![]() )(33m),
)(33m),
解得:m1=14(舍),m2=15,
∴B(![]() ,
, ![]() ),
),
∴BD=2BF=2×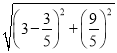 =6,
=6,
则对角线BD的最小值是6;
故答案为:6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x-1=0,②
 ③x-(3x+1)=-5 中,不等组
③x-(3x+1)=-5 中,不等组 的关联方程是________
的关联方程是________ (2)若不等式组
 的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可) (3)若方程 3-x=2x,3+x=
 都是关于 x 的不等式组
都是关于 x 的不等式组 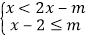 的关联方程,直接写出 m 的取值范围.
的关联方程,直接写出 m 的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是________ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】”切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外作业时间,随机抽取部分学生进行问卷调查,并将调查结果分为A、B、C、D四个等级,A:1小时以内;B:1小时﹣﹣1.5小时;C:1.5小时﹣﹣2小时;D:2小时以上.根据调查结果绘制了如图所示的两种不完整的统计图,
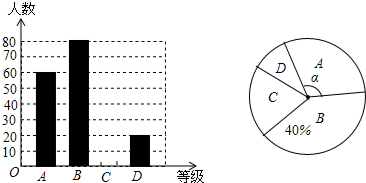
请根据图中信息解答下列问题:
(1)该校共调查了学生;
(2)请将条形统计图补充完整;
(3)表示等级A的扇形圆心角α的度数是;
(4)在此次调查问卷中,甲、乙两班各有2人平均每天课外作业量都是2小时以上,从这4人中人选2人去参加座谈,用列表表或画树状图的方法求选出的2人来自不同班级的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,
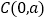 ,
,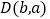 ,其中a、b满足关系式:
,其中a、b满足关系式: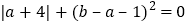 .
.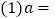 ______,
______,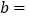 ______,
______,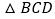 的面积为______;
的面积为______;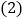 如图2,石
如图2,石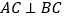 于点C,点P是线段OC上一点,连接BP,延长BP交AC于点
于点C,点P是线段OC上一点,连接BP,延长BP交AC于点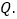 当
当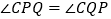 时,求证:BP平分
时,求证:BP平分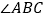 ;
;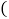 提示:三角形三个内角和等于
提示:三角形三个内角和等于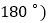
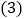 如图3,若
如图3,若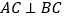 ,点E是点A与点B之间上一点连接CE,且CB平分
,点E是点A与点B之间上一点连接CE,且CB平分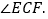 问
问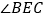 与
与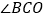 有什么数量关系?请写出它们之间的数量关系并请说明理由.
有什么数量关系?请写出它们之间的数量关系并请说明理由.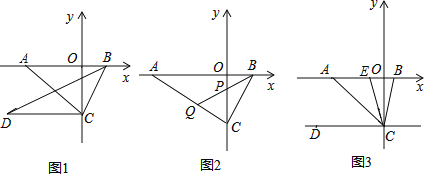
-
科目: 来源: 题型:
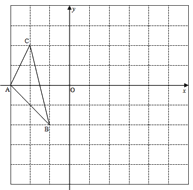
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为:A(-3,0),B(-1,-2),C(-2,2).
(1)请在图中画出△ABC绕B点顺时针旋转90°后的图形△A′BC′.
(2)请直接写出以A′、B、C′为顶点平行四边形的第4个顶点D的坐标.
-
科目: 来源: 题型:
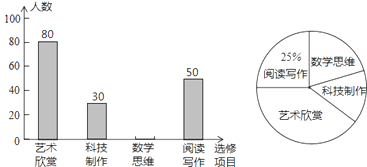
查看答案和解析>>【题目】梅岭中学为了解“课程选修”的情况,对报名参加“艺术欣赏”,“科技制作”,“数学思维”,“阅读写作”这四个选修项目的学生(每人限报一课)进行抽样调查,下面是根据收集的数据绘制的不完整的统计图,请根据图中提供的信息,解答下面的问题:
(1)此次共调查了______名学生,扇形统计图中“艺术欣赏”部分的圆心角是______度;
(2)请把这个条形统计图补充完整;
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修 “科技制作”项目.
相关试题

