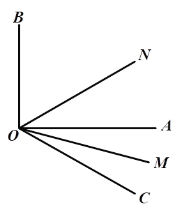
【题目】如图∠AOB是直角,在∠AOB外作射线OC,OM平分∠AOC,ON平分∠BOC.
(1)若∠AOC=38°,求∠MON的度数;
(2)若∠AOC=![]() ,试说明∠MON的大小与
,试说明∠MON的大小与![]() 无关.
无关.
参考答案:
【答案】(1)45°;(2)见解析.
【解析】
(1)先求出∠BOC,再根据角平分线的定义求出∠COM、∠CON,然后根据∠MON=∠CON-∠COM,代入数据进行计算即可得解;
(2)根据(1)的思路,先用含![]() 的式子表示出∠BOC,再根据角平分线的定义求出∠COM、∠CON,然后根据∠MON=∠CON-∠COM,代入数据进行计算即可得解.
的式子表示出∠BOC,再根据角平分线的定义求出∠COM、∠CON,然后根据∠MON=∠CON-∠COM,代入数据进行计算即可得解.
解:(1)∵∠AOB是直角,∠AOC=38°,
∴∠BOC=∠AOB+∠AOC=90°+38°=128°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠COM= ![]() ∠AOC=
∠AOC= ![]() ×38°=19°,
×38°=19°,
∠CON= ![]() ∠BOC=
∠BOC= ![]() ×128°=64°,
×128°=64°,
∴∠MON=∠CON-∠COM,
=64°-19°,
=45°;
(2)∵∠AOB是直角,∠AOC=α,
∴∠BOC=∠AOB+∠AOC=90°+α,
∵OM平分∠AOC,ON平分∠BOC,
∴∠COM= ![]() ∠AOC=
∠AOC= ![]() α,
α,
∠CON= ![]() ∠BOC=
∠BOC= ![]() (90°+α)=45°+
(90°+α)=45°+ ![]() α,
α,
∴∠MON=45°+ ![]() α-
α- ![]() α=45°;
α=45°;
故∠MON的大小与α无关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放
 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数图象经过(6,
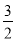 )、(2,
)、(2, )两点.
)两点.
(1)求函数解析式;
(2)该函数图象与x、y轴分别交于A、B两点,点P
 是该函数图象第一象限内的一点,当△OAP的面积为12时,求点P的坐标.
是该函数图象第一象限内的一点,当△OAP的面积为12时,求点P的坐标. -
科目: 来源: 题型:
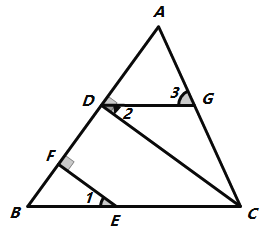
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D. 点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求的∠3度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列表格给出的信息,探究y与x的关系:
x
-4
-3
-2
-1
0
1
2
3
4
y
4
3
2
1
0
1
2
3
4
(1)写出y与x的函数关系式为____________;
(2)在下面的平面直角坐标系中,画出该函数的图象;
(3)根据图象说出y随x的变化规律,若函数y的值有最大(或小)值,直接写出y的最大(或小)值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
材料1:数学上有一种根号内又带根号的数,它们能通过完全平方式及二次根式的性质化去一层(或多层)根号.如:
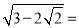
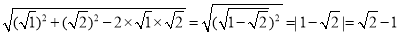 ;
;材料2: 配方法是初中数学思想方法中的一种重要的解题方法。配方法的最终目的就是配成完全平方式,利用完全平方式来解决问题。它的应用非常广泛,在解方程、求最值、证明等式、化简根式、因式分解等方面都经常用到。
如:
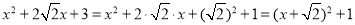
∵
 ,∴
,∴ 即
即
∴
 的最小值为1.
的最小值为1.根据以上材料解决下列问题:
(1)填空:
 =________________;
=________________;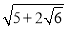 =______________;
=______________;(2)求
 的最小值;
的最小值;(3)已知
 ,求
,求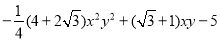 的最大值.
的最大值. -
科目: 来源: 题型:
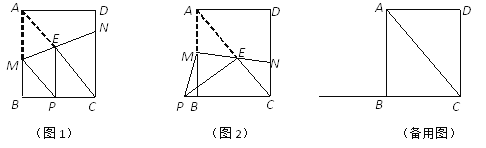
查看答案和解析>>【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.
相关试题

