【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
参考答案:
【答案】问题1:A、B两型自行车的单价分别是70元和80元;问题2:a的值为15.
【解析】
试题分析:问题1:设A型车的成本单价为x元,则B型车的成本单价为(x+10)元,根据成本共计7500元,列方程求解即可;问题2:根据两个街区共有15万人,列出分式方程进行求解并检验即可.
试题解析:
问题1
设A型车的成本单价为x元,则B型车的成本单价为(x+10)元,依题意得
50x+50(x+10)=7500,
解得x=70,
∴x+10=80,
答:A、B两型自行车的单价分别是70元和80元;
问题2
由题可得,![]() ×1000+
×1000+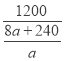 ×1000=150000,
×1000=150000,
解得a=15,
经检验:a=15是所列方程的解,
故a的值为15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,M、N是对角线BD上两点,且BN=DM.
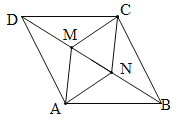
(1)求证:AM=CN;
(2)若AM⊥BD于M,AD=10,CN=6,求DM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:

请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
(1)求证:四边形ACBP是菱形;

(2)若⊙O半径为1,求菱形ACBP的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数图象经过(6,
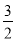 )、(2,
)、(2, )两点.
)两点.
(1)求函数解析式;
(2)该函数图象与x、y轴分别交于A、B两点,点P
 是该函数图象第一象限内的一点,当△OAP的面积为12时,求点P的坐标.
是该函数图象第一象限内的一点,当△OAP的面积为12时,求点P的坐标. -
科目: 来源: 题型:
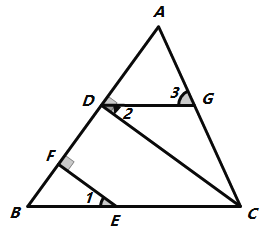
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D. 点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求的∠3度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图∠AOB是直角,在∠AOB外作射线OC,OM平分∠AOC,ON平分∠BOC.
(1)若∠AOC=38°,求∠MON的度数;
(2)若∠AOC=
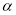 ,试说明∠MON的大小与
,试说明∠MON的大小与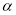 无关.
无关.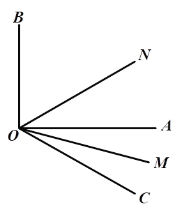
相关试题

