【题目】如图,在Rt△ABC中,∠C=30°,将△ABC绕点B旋转α(0<α<60°)到△A′BC′,边AC和边A′C′相交于点P,边AC和边BC′相交于Q.当△BPQ为等腰三角形时,则α=__________.

参考答案:
【答案】20°或40°
【解析】
过B作BD⊥AC于D,过B作BE⊥A'C'于E,根据旋转可得△ABC≌△A'BC',则BD=BE,进而得到BP平分∠A'PC,再根据∠C=∠C'=30°,∠BQC=∠PQC',可得∠CBQ=∠C'PQ=θ,即可得出∠BPQ=![]() (180°-∠C'PQ)=90°-
(180°-∠C'PQ)=90°-![]() θ,分三种情况讨论,利用三角形内角和等于180°,即可得到关于θ的方程,进而得到结果.
θ,分三种情况讨论,利用三角形内角和等于180°,即可得到关于θ的方程,进而得到结果.
如图,过B作BD⊥AC于D,过B作BE⊥A'C'于E,
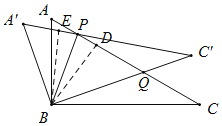
由旋转可得,△ABC≌△A'BC',则BD=BE,
∴BP平分∠A'PC,
又∵∠C=∠C'=30°,∠BQC=∠PQC',
∴∠CBQ=∠C'PQ=θ,
∴∠BPQ=![]() (180°-∠C'PQ)=90°-
(180°-∠C'PQ)=90°-![]() θ,
θ,
分三种情况:
①如图所示,当PB=PQ时,∠PBQ=∠PQB=∠C+∠QBC=30°+θ,
∵∠BPQ+∠PBQ+∠PQB=180°,
∴90°-![]() θ+2×(30°+θ)=180°,
θ+2×(30°+θ)=180°,
解得θ=20°;
②如图所示,当BP=BQ时,∠BPQ=∠BQP,
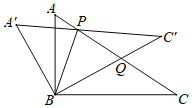
即90°-![]() θ=30°+θ,
θ=30°+θ,
解得θ=40°;
③当QP=QB时,∠QPB=∠QBP=90°-![]() θ,
θ,
又∵∠BQP=30°+θ,
∴∠BPQ+∠PBQ+∠BQP=2(90°-![]() θ)+30°+θ=210°>180°(不合题意),
θ)+30°+θ=210°>180°(不合题意),
故答案为:20°或40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=
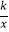 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACB=90°,AC=BC,点C(1,2)、A(-2,0),则点B的坐标是__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如下数表是由从1开始的连续自然数组成的,观察规律并填空:

(1)表中第8行的最后一个数是______,它是自然数_____的平方,第8行共有_____个数;
(2)用含n的代数式表示:第n行的第一个数是___________,最后一个数是_____,第n行共有_________个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;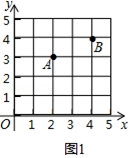
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(2,2),B(4,1),C(4,4).

(1)作出 ABC关于原点O成中心对称的
ABC关于原点O成中心对称的  A1B1C1.
A1B1C1.
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 A1B1C1的内部(不包括顶点和边界),求a的取值范围.
A1B1C1的内部(不包括顶点和边界),求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,CD=CB,若∠ACD=42°,求∠A的度数.

相关试题

