【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.
参考答案:
【答案】(-1,-6)
【解析】解:作BF⊥AC于点F,作AE⊥y轴于点E,设AC交y轴于点D,
∵A(2,3),B(0,2)
∴AE=2,BE=1,
∴AB=![]() ,
,
又∵∠BAC=45°,
∴BF=AF=![]() ,
,
∴△DEA∽△DFB,令AD=x,
∴ ![]() =
=![]() ,
,
∴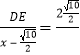
∴DE=![]()
又∵![]()
解得![]() =2
=2![]() ,
,![]() =
=![]() (舍去)
(舍去)
∴AD=2![]() ,
,
设D(0,y)
∴![]() +4=
+4=![]()
解得:![]() =-3,
=-3,![]() =9(舍去)
=9(舍去)
∴设AC直线方程为y=kx+b,将A(2,3),D(0,-3)代入直线方程得,![]() ;解得
;解得![]()
∴AC:y=3x-3,
∵A(2,3)在y=![]() 上,
上,
∴k=2×3=6,
∴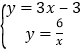 ;解得
;解得![]() ;
;
∴C(-1,-6).
【考点精析】掌握确定一次函数的表达式和勾股定理的概念是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).

(1)用的代数式表示PC的长度;
(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=-x+m分别交于x轴、y轴于A,B两点,已知点C(2,0).
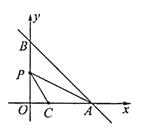
(1)当直线AB经过点C时,点O到直线AB的距离是;
(2)设点P为线段OB的中点,连结PA,PC,若∠CPA=∠ABO,则m的值是. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D,且AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )

A. 80° B. 70° C. 60° D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACB=90°,AC=BC,点C(1,2)、A(-2,0),则点B的坐标是__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如下数表是由从1开始的连续自然数组成的,观察规律并填空:

(1)表中第8行的最后一个数是______,它是自然数_____的平方,第8行共有_____个数;
(2)用含n的代数式表示:第n行的第一个数是___________,最后一个数是_____,第n行共有_________个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=30°,将△ABC绕点B旋转α(0<α<60°)到△A′BC′,边AC和边A′C′相交于点P,边AC和边BC′相交于Q.当△BPQ为等腰三角形时,则α=__________.

相关试题

