【题目】如图,在△ABC中,AB=AC,CD=CB,若∠ACD=42°,求∠A的度数.

参考答案:
【答案】∠A=32°.
【解析】
设∠BAC=x,根据等边对等角及三角形外角的性质得出∠B=∠BDC=42°+x,∠ADC=∠B+∠BCD=42°+x+x=42°+2x,再根据邻补角定义得出∠ADC+∠BDC=180°,由此列出方程42°+2x+42°+x=180°,解方程即可.
设∠BAC=x,则∠BDC=42°+x.
∵CD=CB,
∴∠B=∠BDC=42°+x.
∵AB=AC,
∴∠ACB=∠B=42°+x,
∴∠BCD=∠ACB-∠ACD=x,
∴∠ADC=∠B+∠BCD=42°+x+x=42°+2x.
∵∠ADC+∠BDC=180°,
∴42°+2x+42°+x=180°,
解得x=32°,
所以∠BAC═32°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=30°,将△ABC绕点B旋转α(0<α<60°)到△A′BC′,边AC和边A′C′相交于点P,边AC和边BC′相交于Q.当△BPQ为等腰三角形时,则α=__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;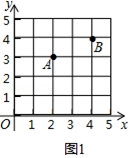
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.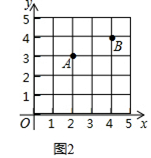
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(2,2),B(4,1),C(4,4).

(1)作出 ABC关于原点O成中心对称的
ABC关于原点O成中心对称的  A1B1C1.
A1B1C1.
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 A1B1C1的内部(不包括顶点和边界),求a的取值范围.
A1B1C1的内部(不包括顶点和边界),求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是2018年12月份的日历,我们选择其中的方框部分,将每个方框部分中4个位置上的数交叉求平方和,再相减,例如:(32+112)-(42+102)=14,(212+292)-(222+282)=14,不难发现结果都是14.
(1)今天是12月12日,请你写一个含今天日期在内的类似部分的算式;
(2)请你利用整式的运算对以上规律加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
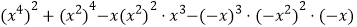 ;
;(2)
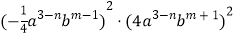 ;
;(3)
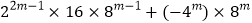 (m为正整数).
(m为正整数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
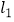 :
: 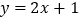 与直线
与直线 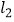 :
: 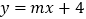 相交于点P(1,b)
相交于点P(1,b)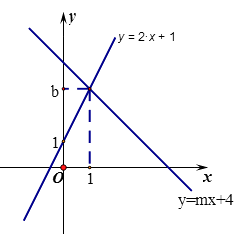
(1)求b,m的值
(2)垂直于x轴的直线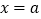 与直线
与直线 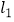 ,
, 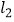 分别相交于C,D,若线段CD长为2,求a的值
分别相交于C,D,若线段CD长为2,求a的值
相关试题

