【题目】如图,∠ACB=90°,AC=BC,点C(1,2)、A(-2,0),则点B的坐标是__________.

参考答案:
【答案】(3,-1)
【解析】
过C和B分别作CD⊥OD于D,BE⊥CD于E,利用已知条件可证明△ADC≌△CEB,再由全等三角形的性质和已知数据即可求出B点的坐标.
过C和B分别作CD⊥OD于D,BE⊥CD于E,
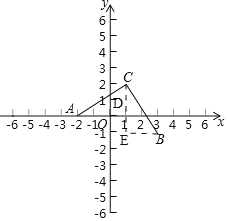
∵∠ACB=90°,
∴∠ACD+∠CAD=90°,∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
∠ADC=∠CEB=90°;∠CAD=∠BCE,AC=BC,
∴△ADC≌△CEB(AAS),
∴DC=BE,AD=CE,
∵点C的坐标为(1,2),点A的坐标为(2,0),
∴AD=CE=3,OD=1,BE=CD=2,
∴则B点的坐标是(3,1).
故答案为:(3,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从表可知,
①抛物线与x轴的交点为;
②抛物线的对称轴是;
③函数y=ax2+bx+c的最大值为;
④x , y随x增大而增大. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
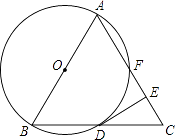
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形 ABCD 中, AB = a, BC = b, a > b .以 AB 边为轴将长方形旋转一周形成 圆柱体甲,再以 BC 边为轴将长方形旋转一周形成圆柱体乙.记两个圆柱体的体积分别为 V甲 ,V乙 ,侧面积分别为 S甲, S乙 ,则下列正确的是( )
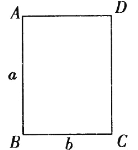
A. V甲 > V乙 , S甲=S乙
B. V甲 < V乙 , S甲= S乙
C. V甲= V乙 , S甲= S乙
D. V甲 > V乙 , S甲 < S乙
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;
(2)用五点法画出此函数图象的示意图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
相关试题

