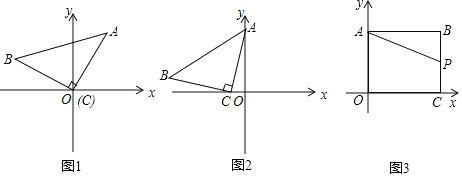
【题目】![]() 操作思考:如图1,在平面直角坐标系中,等腰
操作思考:如图1,在平面直角坐标系中,等腰![]() 的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点
的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点![]() 处
处![]() 则
则![]() 的长为______;
的长为______;![]() 点B的坐标为______
点B的坐标为______![]() 直接写结果
直接写结果![]()
![]() 感悟应用:如图2,在平面直角坐标系中,将等腰
感悟应用:如图2,在平面直角坐标系中,将等腰![]() 如图放置,直角顶点
如图放置,直角顶点![]() ,点
,点![]() ,试求直线AB的函数表达式.
,试求直线AB的函数表达式.
![]() 拓展研究:如图3,在直角坐标系中,点
拓展研究:如图3,在直角坐标系中,点![]() ,过点B作
,过点B作![]() 轴,垂足为点A,作
轴,垂足为点A,作![]() 轴,垂足为点C,P是线段BC上的一个动点,点Q是直线
轴,垂足为点C,P是线段BC上的一个动点,点Q是直线![]() 上一动点
上一动点![]() 问是否存在以点P为直角顶点的等腰
问是否存在以点P为直角顶点的等腰![]() ,若存在,请求出此时P的坐标,若不存在,请说明理由.
,若存在,请求出此时P的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)
(3)![]() ,
,![]()
【解析】
![]() 由
由![]() 可得,
可得,![]() ,
,![]() ,
,![]() ,易证
,易证![]() ≌
≌![]() ,
,![]() ,
,![]() ,因此
,因此![]() ;
;
![]() 同
同![]() 可证
可证![]() ≌
≌![]() ,
,![]() ,
,![]() ,
,![]() ,求得
,求得![]() 最后代入求出一次函数解析式即可;
最后代入求出一次函数解析式即可;
![]() 分两种情况讨论
分两种情况讨论![]() 当点Q在x轴下方时,
当点Q在x轴下方时,![]() 当点Q在x轴上方时
当点Q在x轴上方时![]() 根据等腰
根据等腰![]() 构建一线三直角,从而求解.
构建一线三直角,从而求解.
![]() 如图1,作
如图1,作![]() 轴,
轴,![]() 轴.
轴.
![]() ,
,
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
故答案为![]() ,
,![]() ;
;
![]() 如图2,过点B作
如图2,过点B作![]() 轴.
轴.
![]() ,
,![]()
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() .
.
设直线AB的表达式为![]()
将![]() 和
和![]() 代入,得
代入,得
![]() ,
,
解得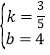 ,
,
![]() 直线AB的函数表达式
直线AB的函数表达式![]() .
.
![]() 如图3,设
如图3,设![]() ,分两种情况:
,分两种情况:
![]() 当点Q在x轴下方时,
当点Q在x轴下方时,![]() 轴,与BP的延长线交于点
轴,与BP的延长线交于点![]() .
.
![]() ,
,
![]() ,
,
![]()
在![]() 与
与![]() 中
中
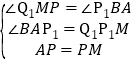
![]() ≌
≌![]()
![]() ,
,![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
解得![]()
![]()
此时点P与点C重合,
![]() ;
;
![]() 当点Q在x轴上方时,
当点Q在x轴上方时,![]() 轴,与PB的延长线交于点
轴,与PB的延长线交于点![]() .
.
同理可证![]() ≌
≌![]() .
.
同理求得![]()
综上,P的坐标为:![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解并解答:
为了求1+2+22+23+24+…+22009的值.
可令S=1+2+22+23+24+…+22009
则2S=2+22+23+24+…+22009+22010
因此2S﹣S=(2+22+23+24+…+22009+22010)﹣(1+22+23+24+…+22009)=22010﹣1
所以S=22010﹣1即1+2+22+23+24+…+22009=22010﹣1
请依照此法,求:1+5+52+53+54+…+52020的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电信公司推出甲、乙两种收费方式供手机用户选择:
甲种方式:每月收月租费5元,每分钟通话费为
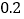 元;
元;乙种方式:不收月租费,每分钟通话费为
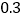 元;
元;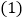 请分别写出甲乙两种收费方式每月付费
请分别写出甲乙两种收费方式每月付费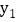 、
、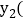 元
元 与通话时间
与通话时间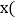 分钟
分钟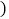 之间函数表达式;
之间函数表达式; 如何根据通话时间的多少选择付费方式,请给出你的方案.
如何根据通话时间的多少选择付费方式,请给出你的方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为6cm的⊙O中,点A是劣弧
 的中点,点D是优弧
的中点,点D是优弧  上一点,且∠D=30°,下列四个结论:
上一点,且∠D=30°,下列四个结论:
①OA⊥BC;②BC=6 ;③sin∠AOB=
;③sin∠AOB=  ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.
其中正确结论的序号是( )
A.①③
B.①②③④
C.②③④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过两种不同的方式计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.

例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图2,可得等式 ;
(2)利用(1)所得等式,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长为a、b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF,若这两个正方形的边长a、b如图标注,且满足a+b=10,ab=20.请求出阴影部分的面积.
(4)图4中给出了边长分别为a、b的小正方形纸片和两边长分别为a、b的长方形纸片,现有足量的这三种纸片.
①请在下面的方框中用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形,并仿照图1、图2画出拼法并标注a、b;

②研究①拼图发现,可以分解因式2a2+5ab+2b2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量
 (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程 (千米)的函数图象.
(千米)的函数图象.
(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求
 关于
关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
相关试题

