【题目】如图,在![]() 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,
(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.

参考答案:
【答案】(1)18 (2)EF垂直平分AD,理由见解析
【解析】试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得DE=AE=![]() AB,DF=AF=
AB,DF=AF=![]() AC,再根据四边形的周长的定义计算即可得解;
AC,再根据四边形的周长的定义计算即可得解;
(2)根据到到线段两端点距离相等的点在线段的垂直平分线上证明即可.
试题解析:(1)∵AD是高,E、F分别是AB、AC的中点,
∴DE=AE=![]() AB=
AB=![]() ×10=5,DF=AF=
×10=5,DF=AF=![]() AC=
AC=![]() ×8=4,
×8=4,
∴四边形AEDF的周长=AE+DE+DF+AF=5+5+4+4=18;
(2)EF垂直平分AD.
证明:∵DE=AE,DF=AF,
∴EF垂直平分AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(
 )﹣3﹣20160﹣|﹣5|;
)﹣3﹣20160﹣|﹣5|;(2)(3a2)2﹣a22a2+(﹣2a3)2+a2;
(3)(x+5)2﹣(x﹣2)(x﹣3);
(4)(2x+y﹣2)(2x+y+2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两人利用不同的交通工具,沿同一路线从A地出发到距离A地350千米的B地办事,甲先出发,乙后出发,甲、乙两人距A地的路程和时间的关系如图所示,根据图示提供的信息解答:
 乙比甲晚______小时出发;乙出发______小时后追上甲;
乙比甲晚______小时出发;乙出发______小时后追上甲; 分别求甲、乙两人离开A地的路程s关于t的函数关系式;
分别求甲、乙两人离开A地的路程s关于t的函数关系式; 求乙比甲早几小时到达B地?
求乙比甲早几小时到达B地?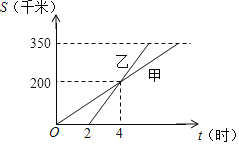
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解并解答:
为了求1+2+22+23+24+…+22009的值.
可令S=1+2+22+23+24+…+22009
则2S=2+22+23+24+…+22009+22010
因此2S﹣S=(2+22+23+24+…+22009+22010)﹣(1+22+23+24+…+22009)=22010﹣1
所以S=22010﹣1即1+2+22+23+24+…+22009=22010﹣1
请依照此法,求:1+5+52+53+54+…+52020的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电信公司推出甲、乙两种收费方式供手机用户选择:
甲种方式:每月收月租费5元,每分钟通话费为
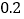 元;
元;乙种方式:不收月租费,每分钟通话费为
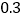 元;
元; 请分别写出甲乙两种收费方式每月付费
请分别写出甲乙两种收费方式每月付费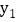 、
、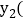 元
元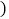 与通话时间
与通话时间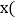 分钟
分钟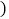 之间函数表达式;
之间函数表达式;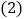 如何根据通话时间的多少选择付费方式,请给出你的方案.
如何根据通话时间的多少选择付费方式,请给出你的方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】
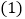 操作思考:如图1,在平面直角坐标系中,等腰
操作思考:如图1,在平面直角坐标系中,等腰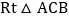 的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点
的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点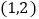 处
处 则
则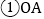 的长为______;
的长为______; 点B的坐标为______
点B的坐标为______ 直接写结果
直接写结果
 感悟应用:如图2,在平面直角坐标系中,将等腰
感悟应用:如图2,在平面直角坐标系中,将等腰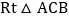 如图放置,直角顶点
如图放置,直角顶点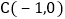 ,点
,点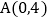 ,试求直线AB的函数表达式.
,试求直线AB的函数表达式.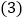 拓展研究:如图3,在直角坐标系中,点
拓展研究:如图3,在直角坐标系中,点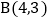 ,过点B作
,过点B作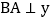 轴,垂足为点A,作
轴,垂足为点A,作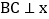 轴,垂足为点C,P是线段BC上的一个动点,点Q是直线
轴,垂足为点C,P是线段BC上的一个动点,点Q是直线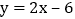 上一动点
上一动点 问是否存在以点P为直角顶点的等腰
问是否存在以点P为直角顶点的等腰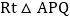 ,若存在,请求出此时P的坐标,若不存在,请说明理由.
,若存在,请求出此时P的坐标,若不存在,请说明理由.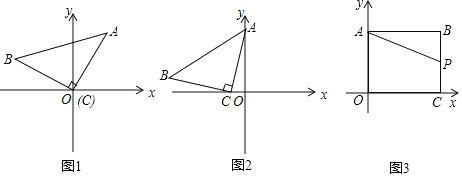
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为6cm的⊙O中,点A是劣弧
 的中点,点D是优弧
的中点,点D是优弧  上一点,且∠D=30°,下列四个结论:
上一点,且∠D=30°,下列四个结论:
①OA⊥BC;②BC=6 ;③sin∠AOB=
;③sin∠AOB=  ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.
其中正确结论的序号是( )
A.①③
B.①②③④
C.②③④
D.①③④
相关试题

