【题目】如图,下面不能判断是平行四边形的是( )

A. ∠B=∠D,∠BAD=∠BCD
B. AB∥CD,AD=BC
C. ∠B+∠DAB=180°,∠B+∠BCD=180°
D. AB∥CD,AB=CD
参考答案:
【答案】B
【解析】
由平行四边形的判定方法得出选项A、C、D正确,选项B不正确,即可得出结论.
解:∵∠B=∠D,∠BAD=∠BCD,
∴四边形ABCD是平行四边形,A选项正确;
∵AB∥CD,AD=BC,
∴四边形ABCD是等腰梯形,
不一定是平行四边形,B选项不正确;
∵∠B+∠DAB=180°,∠B+∠BCD=180°,
∴AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,C选项正确;
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,D选项正确.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富同学们的课余生活,某校决定在七年级学生中开展足球、篮球、乒乓球以及羽毛球四项课外体育活动,并要求每名学生必须且只能选择其中一项
 为了提前了解选择各种体育项目的学生人数,作为校学生会体育部部长的小强,随机抽取了部分七年级学生进行问卷调查,并绘制出了以下两幅不完整的统计图
为了提前了解选择各种体育项目的学生人数,作为校学生会体育部部长的小强,随机抽取了部分七年级学生进行问卷调查,并绘制出了以下两幅不完整的统计图 请根据统计图回答下列问题
请根据统计图回答下列问题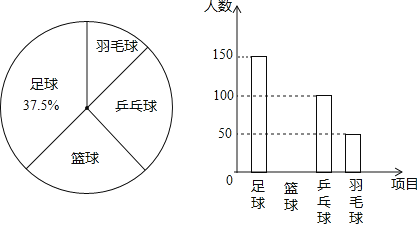
 参与问卷调查的学生有多少人?并补全条形统计图;
参与问卷调查的学生有多少人?并补全条形统计图; 在扇形统计图中,选择乒乓球项目的扇形的圆心角是多少度?
在扇形统计图中,选择乒乓球项目的扇形的圆心角是多少度? 若该校七年级总人数为1200人,请估计选择羽毛球项目的人数一共是多少人?
若该校七年级总人数为1200人,请估计选择羽毛球项目的人数一共是多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+b与反比例函数y=
 (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN= ,求t的值.
,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是直径,直线MN过点B,且∠MBC=∠BAC.半径OD⊥BC,垂足为H,AD交BC于点G,DE⊥AB于点E,交BC于点F.
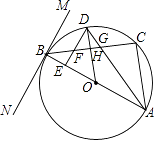
(1)求证:MN是⊙O的切线;
(2)求证:DE= BC;
BC;
(3)若tan∠CAG= ,DG=4,求点F到直线AD的距离.
,DG=4,求点F到直线AD的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.
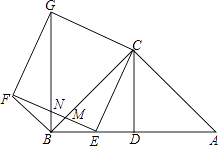
(1)证明:△CAE≌△CBG;
(2)设DE=x,BN=y,求y关于x的函数关系式,并求出y的最大值;
(3)当DE=2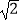 ﹣2时,求∠BFE的度数.
﹣2时,求∠BFE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个自色六边形相邻,若一段边框上有25个黑色六边形,则这段边框共有白色六边形

A. 100个 B. 102个 C. 98个 D. 150个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为
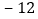 和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.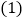 当
当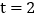 时,
时,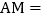 ______个单位长度,
______个单位长度,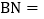 ______个单位长度,此时MN的中点C所对应的有理数为______;
______个单位长度,此时MN的中点C所对应的有理数为______;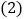 在运动过程中,当
在运动过程中,当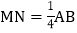 时,求点M所对应的有理数.
时,求点M所对应的有理数.
相关试题

