【题目】为了丰富同学们的课余生活,某校决定在七年级学生中开展足球、篮球、乒乓球以及羽毛球四项课外体育活动,并要求每名学生必须且只能选择其中一项![]() 为了提前了解选择各种体育项目的学生人数,作为校学生会体育部部长的小强,随机抽取了部分七年级学生进行问卷调查,并绘制出了以下两幅不完整的统计图
为了提前了解选择各种体育项目的学生人数,作为校学生会体育部部长的小强,随机抽取了部分七年级学生进行问卷调查,并绘制出了以下两幅不完整的统计图![]() 请根据统计图回答下列问题
请根据统计图回答下列问题
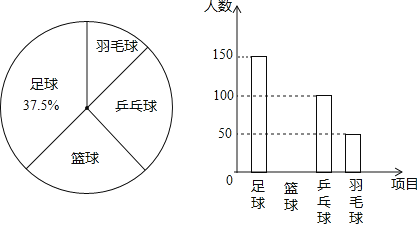
![]() 参与问卷调查的学生有多少人?并补全条形统计图;
参与问卷调查的学生有多少人?并补全条形统计图;
![]() 在扇形统计图中,选择乒乓球项目的扇形的圆心角是多少度?
在扇形统计图中,选择乒乓球项目的扇形的圆心角是多少度?
![]() 若该校七年级总人数为1200人,请估计选择羽毛球项目的人数一共是多少人?
若该校七年级总人数为1200人,请估计选择羽毛球项目的人数一共是多少人?
参考答案:
【答案】![]() 参与问卷调查的学生有
参与问卷调查的学生有![]() 人,补全条形图见解析;
人,补全条形图见解析;![]() 选择乒乓球项目的扇形的圆心角是
选择乒乓球项目的扇形的圆心角是![]() ;
;![]() 选择羽毛球项目的人数一共是150人.
选择羽毛球项目的人数一共是150人.
【解析】
(1)用足球的人数除以其所占百分比可得总人数,再根据各项目的人数之和等于总人数求得篮球的人数即可补全条形图;
(2)用360°乘以乒乓球的人数占被调查人数的比例即可得;
(3)用总人数乘以样本中羽毛球的人数所占比例即可得.
(1)参与问卷调查的学生有150÷37.5%=400(人),则篮球的人数为:400﹣(150+100+50)=100(人),补全条形图如下:
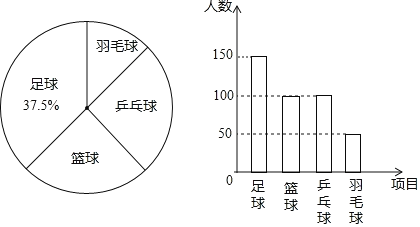
(2)选择乒乓球项目的扇形的圆心角是360°![]() 90°;
90°;
(3)估计选择羽毛球项目的人数一共是1200![]() 150(人).
150(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内有一点D,且DA=DB=DC.若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )

A. 100° B. 80° C. 70° D. 50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣1,1)、B(4,6)在抛物线y=ax2+bx上
(1)求抛物线的解析式;
(2)如图1,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH、AE,求证:FH∥AE;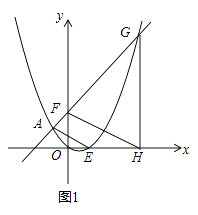
(3)如图2,直线AB分别交x轴、y轴于C、D两点.点P从点C出发,沿射线CD方向匀速运动,速度为每秒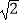
个单位长度;同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度.点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=2PM,直接写出t的值.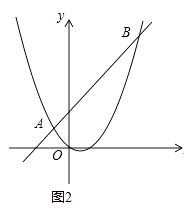
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于不等式组
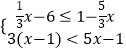 ,下列说法正确的是( )
,下列说法正确的是( )
A.此不等式组的正整数解为1,2,3
B.此不等式组的解集为﹣1<x≤
C.此不等式组有5个整数解
D.此不等式组无解 -
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+b与反比例函数y=
 (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN= ,求t的值.
,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是直径,直线MN过点B,且∠MBC=∠BAC.半径OD⊥BC,垂足为H,AD交BC于点G,DE⊥AB于点E,交BC于点F.
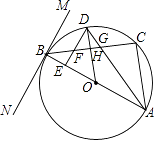
(1)求证:MN是⊙O的切线;
(2)求证:DE= BC;
BC;
(3)若tan∠CAG= ,DG=4,求点F到直线AD的距离.
,DG=4,求点F到直线AD的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下面不能判断是平行四边形的是( )

A. ∠B=∠D,∠BAD=∠BCD
B. AB∥CD,AD=BC
C. ∠B+∠DAB=180°,∠B+∠BCD=180°
D. AB∥CD,AB=CD
相关试题

