【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为![]() 和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
![]() 当
当![]() 时,
时,![]() ______个单位长度,
______个单位长度,![]() ______个单位长度,此时MN的中点C所对应的有理数为______;
______个单位长度,此时MN的中点C所对应的有理数为______;
![]() 在运动过程中,当
在运动过程中,当![]() 时,求点M所对应的有理数.
时,求点M所对应的有理数.
![]()
参考答案:
【答案】(1)6,4,![]() ;(2)
;(2)![]() 时,M对应数字是3或
时,M对应数字是3或![]() .
.
【解析】
(1)AM=3t,BN=2t,表示出M,N所表示的数字,二者和的一半即中点C对应数字;
(2)分M在右边,N在左边和M在左边,N在右边两种可能.用t表示MN的长度,根据MN![]() AB列方程求解.
AB列方程求解.
(1)M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,t秒后,AM=3t,MN=2t,当t=2时,AM=6,BN=4,此时M、N对应数字是﹣6和4,所以MN![]() .
.
故答案为:6,4,﹣1;
(2)M、N对应数字是﹣12+3t和8﹣2t.
当M在左边,N在右边时,MN=8﹣2t﹣(﹣12+3t)=20﹣5t.
∵MN![]() AB,∴20﹣5t
AB,∴20﹣5t![]() ,∴t=3,所以此时M对应数字是﹣3;
,∴t=3,所以此时M对应数字是﹣3;
当M在右边,N在左边时,MN=﹣12+3t﹣(8﹣2t)=﹣20+5t.
∵MN![]() AB,∴﹣20+5t
AB,∴﹣20+5t![]() ,∴t=5,所以此时M对应数字是3.
,∴t=5,所以此时M对应数字是3.
综上所述:当MN![]() AB时,M对应数字是3或﹣3.
AB时,M对应数字是3或﹣3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下面不能判断是平行四边形的是( )

A. ∠B=∠D,∠BAD=∠BCD
B. AB∥CD,AD=BC
C. ∠B+∠DAB=180°,∠B+∠BCD=180°
D. AB∥CD,AB=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.
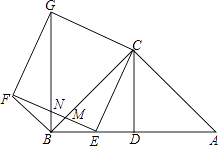
(1)证明:△CAE≌△CBG;
(2)设DE=x,BN=y,求y关于x的函数关系式,并求出y的最大值;
(3)当DE=2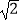 ﹣2时,求∠BFE的度数.
﹣2时,求∠BFE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个自色六边形相邻,若一段边框上有25个黑色六边形,则这段边框共有白色六边形

A. 100个 B. 102个 C. 98个 D. 150个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )
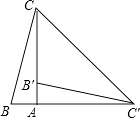
A.32°
B.64°
C.77°
D.87° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=(x+m)2﹣n的图象如图所示,则一次函数y=mx+n与反比例函数y=
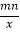 的图象可能是( )
的图象可能是( )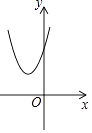
A.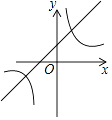
B.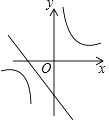
C.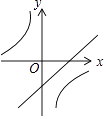
D.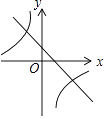
-
科目: 来源: 题型:
查看答案和解析>>【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为
 千克时,运费为
千克时,运费为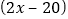 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为 千克时,运费为
千克时,运费为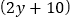 元。
元。(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
相关试题

