【题目】已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.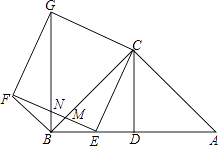
(1)证明:△CAE≌△CBG;
(2)设DE=x,BN=y,求y关于x的函数关系式,并求出y的最大值;
(3)当DE=2 ![]() ﹣2时,求∠BFE的度数.
﹣2时,求∠BFE的度数.
参考答案:
【答案】
(1)证明:∵四边形EFGC是正方形,
∴CG=CE,∠GCE=∠GFE=∠FEC=90°,
∵∠ACB=∠GCE=90°,
∴∠GCB=∠ECA,
∵GC=CE,CB=CA,
∴△CAE≌△CBG.
(2)解:∵CB=CA,CD⊥AB,∠ACB=90°,
∴CD=BD=AD=2,∠CBA=∠A=45°,
∵△CAE≌△CBG,
∴∠CBG=∠A=45°,
∴∠GBA=∠GBC+∠CBA=90°,
∵∠BEN+∠BNE=90°,∠BEN+∠CED=90°,
∴∠BNE=∠CED,∵∠EBN=∠CDE=90°,
∴△NBE∽△EDC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴y=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴x=1时,y的最大值为 ![]() .
.
(3)解:在CD上取一点K,使得DE=DK=2 ![]() ﹣2,
﹣2,
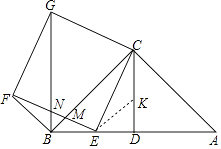
∴EK=4﹣2 ![]() ,
,
∵CK=CD﹣DK=2﹣(2 ![]() ﹣2)=4﹣2
﹣2)=4﹣2 ![]() ,
,
∴KC=EK,
∵∠EKD=∠KED=45°,
∴∠KEC=∠KCE=22.5°,
∴∠CED=67.5°,
∴∠FEB=90°﹣67.5°=22.5°,
∵BE=BD﹣DE=4﹣2 ![]() =EK,CE=EF,∠BEF=∠ECK,
=EK,CE=EF,∠BEF=∠ECK,
∴△BEF≌△KEC,
∴∠EFB=∠ECK=22.5°.
【解析】(1)根据SAS证明即可;(2)只要证明△NBE∽△EDC,可得![]() ,可得
,可得![]() ,由此即可解决问题;(3)在CD上取一点K,使得DE=DK=
,由此即可解决问题;(3)在CD上取一点K,使得DE=DK=![]() ,首先证明KC=EK,再证明△BEF≌△KEC即可解决问题,
,首先证明KC=EK,再证明△BEF≌△KEC即可解决问题,
【考点精析】认真审题,首先需要了解相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方).
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+b与反比例函数y=
 (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN= ,求t的值.
,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是直径,直线MN过点B,且∠MBC=∠BAC.半径OD⊥BC,垂足为H,AD交BC于点G,DE⊥AB于点E,交BC于点F.
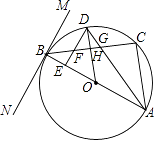
(1)求证:MN是⊙O的切线;
(2)求证:DE= BC;
BC;
(3)若tan∠CAG= ,DG=4,求点F到直线AD的距离.
,DG=4,求点F到直线AD的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下面不能判断是平行四边形的是( )

A. ∠B=∠D,∠BAD=∠BCD
B. AB∥CD,AD=BC
C. ∠B+∠DAB=180°,∠B+∠BCD=180°
D. AB∥CD,AB=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个自色六边形相邻,若一段边框上有25个黑色六边形,则这段边框共有白色六边形

A. 100个 B. 102个 C. 98个 D. 150个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为
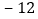 和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.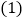 当
当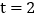 时,
时,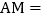 ______个单位长度,
______个单位长度,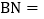 ______个单位长度,此时MN的中点C所对应的有理数为______;
______个单位长度,此时MN的中点C所对应的有理数为______;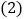 在运动过程中,当
在运动过程中,当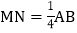 时,求点M所对应的有理数.
时,求点M所对应的有理数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )
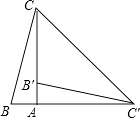
A.32°
B.64°
C.77°
D.87°
相关试题

