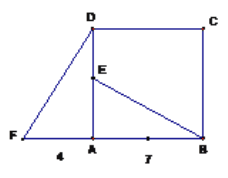
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7.
(1)旋转中心是点 ,旋转了 度,DE的长度是 ;
(2)BE与DF的关系如何? 请说明理由.(提示:延长BE交DF于点G)
参考答案:
【答案】(1)A;90;3;(2)BE⊥DF.
【解析】试题分析:(1)由△ADF绕点A顺时针旋转90度得到△ABE可知AE=AF=4,AD=AB=7,从而得出DE的长;
(2)根据旋转的性质得出∠F=∠AEB=∠DEG,再根据∠F+∠ADF=90°可得∠DEG+∠ADF=90°,即可得答案.
试题解析:解:(1)根据题意可知,△ADF绕点A顺时针旋转90度得到△ABE,∴AE=AF=4,AD=AB=7,∴DE=AD﹣AE=3;
(2)BE⊥DF.理由如下:
如图,延长BE交DF于点G.由旋转的性质可得:∠AEB=∠F,又∵∠AEB=∠DEG,∴∠F=∠DEG,∵∠F+∠ADF=90°,∴∠DEG+∠ADF=90°,∴∠AGE=90°,即BE⊥DF.

-
科目: 来源: 题型:
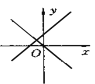
查看答案和解析>>【题目】下图表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且mn
 0)的大致图像是( )
0)的大致图像是( )A.
 B.
B.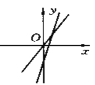
C.
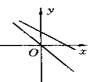 D.
D.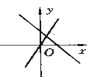
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时; ③乙车出发后2小时追上甲车; ④当甲、乙两车相距50千米时,t=
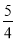 或
或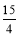 .其中正确的结论有_____.
.其中正确的结论有_____.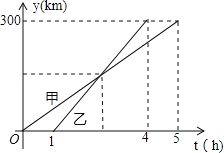
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于X的一元二次方程为:
 。
。(1)当方程有两实数根时,求
 的取值范围;
的取值范围;(2)任取一个
 值,求出方程的两个不相等实数根。
值,求出方程的两个不相等实数根。 -
科目: 来源: 题型:
查看答案和解析>>【题目】依据给定的条件,求一次函数的表达式.
(1)已知一次函数的图象如图所示,求此一次函数的表达式,并判断点(6,5)是否在此函数图象上;
(2)已知直线y=kx+b平行于直线y=3x+4,且过点(1,2),求此直线的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=﹣x+m经过点A(2,0),交y轴于点B.点D为x轴上一点,且S△ADB=1.

(1)求m的值;
(2)求线段OD的长;
(3)当点E在直线AB上(点E与点B不重合),且∠BDO=∠EDA,求点E的坐标.
相关试题

