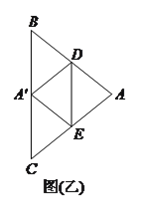
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() .
.
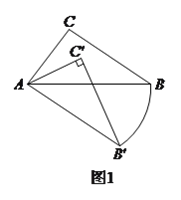
(![]() )把
)把![]() 绕点
绕点![]() 按顺时针方向旋转,得
按顺时针方向旋转,得![]() ,
, ![]() 交
交![]() 于点
于点![]() .
.
①若![]() ,旋转角为
,旋转角为![]() ,求
,求![]() 的长.
的长.
②若点![]() 经过的路径与
经过的路径与![]() ,
, ![]() 所围图形的面积与
所围图形的面积与![]() 面积的比值是
面积的比值是![]() ,求
,求![]() 的度数.
的度数.
(![]() )点
)点![]() 在边
在边![]() 上,
上, ![]() ,把
,把![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 度后,如果点
度后,如果点![]() 恰好落在初始
恰好落在初始![]() 的边上,求
的边上,求![]() 的值.
的值.
参考答案:
【答案】(1)①1;②75°;(2)60°或150°.
【解析】试题分析:(1)①首先求出AC的长,进而得出AC′=AC,∠C′=90°,得出
C′D=AC′·tan30°=1;②利用AB′所围图形的面积与△ABC面积的比值是![]() ,得出n的度数即可;
,得出n的度数即可;
(2)分别根据等边三角形的判定得出,∠APA1=60°,再利用CP:PA=![]() ,得出∠CPA2=30°,即可得出答案.
,得出∠CPA2=30°,即可得出答案.
解:(![]() )①∵
)①∵![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ,而
,而![]() ,
, ![]() ,∴
,∴![]() .
.
②如图![]() ,设
,设![]() ,则
,则![]() ,
, ![]() ,旋转角度数为
,旋转角度数为![]() ,则
,则 ,∴
,∴![]() ,∴
,∴![]() .
.
(![]() )如图
)如图![]() ,∵
,∵![]() ,
, ![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将△ABC作同样的平移得到△A1B1C1的面积.求:
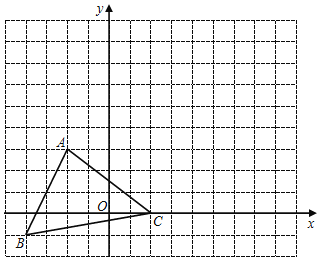
(1)画出△A1B1C1和写出点B1的坐标;
(2)写出平移的过程;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=5,BM=2,AC=9,则∠ABC与∠C的关系为( )

A.∠ABC=2∠CB.∠ABC=
 ∠CC.
∠CC. ∠ABC=∠CD.∠ABC=3∠C
∠ABC=∠CD.∠ABC=3∠C -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 (
( 为非零常数).
为非零常数).(
 )若对称轴是直线
)若对称轴是直线 .
.①求二次函数的解析式.
②二次函数
 (
(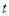 为实数)图象的顶点在
为实数)图象的顶点在 轴上,求
轴上,求 的值.
的值.(
 )把抛物线
)把抛物线 向上平移
向上平移 个单位得到新的抛物线
个单位得到新的抛物线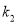 ,若
,若 ,求
,求 的图像落在
的图像落在 轴上方的部分对应的
轴上方的部分对应的 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
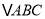 中,
中, 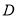 为
为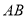 边上一点,过点
边上一点,过点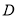 作
作 交
交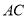 于点
于点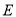 ,以
,以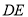 为折线,将
为折线,将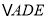 翻折,设所得的
翻折,设所得的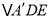 与梯形
与梯形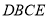 重叠部分的面积为
重叠部分的面积为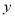 .
.(
 )如图(甲),若
)如图(甲),若 ,
, 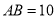 ,
,  ,
, 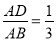 ,则
,则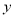 的值为__________.
的值为__________.(
 )如图(乙),若
)如图(乙),若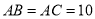 ,
, 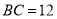 ,
, 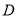 为
为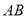 中点,则
中点,则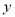 的值为__________.
的值为__________.(
 )若
)若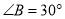 ,
, 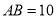 ,
, 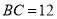 ,设
,设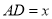 .
.①求
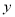 与
与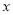 的函数解析式.
的函数解析式.②
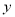 是否有最大值,若有,求出
是否有最大值,若有,求出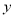 的最大值;若没有,请说明理由.
的最大值;若没有,请说明理由.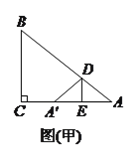
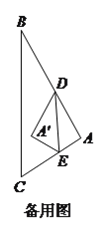
-
科目: 来源: 题型:
查看答案和解析>>【题目】小林在某商店购买商品A、B若干次(每次A、B两种商品都购买),其中第一、二两次购买时,均按标价购买;第三次购买时,商品A、B同时打折.三次购买商品A、B的数量和费用如表所示.
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
980
第二次购物
3
7
940
第三次购物
9
8
912
(1)求商品A、B的标价;
(2)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
(3)在(2)的条件下,若小林第四次购物共花去了960元,则小林有哪几种购买方案?
-
科目: 来源: 题型:
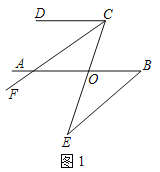
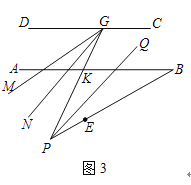
查看答案和解析>>【题目】(1)如图1,AB∥CD,CF平分∠DCE,若∠DCF=30°,∠E=20°,求∠ABE的度数.
(2)如图2,已知AB∥CD,CF平分∠DCE,∠EBF=2∠ABF,若∠F的2倍与∠E的补角的和为190°,求∠ABE的度数.
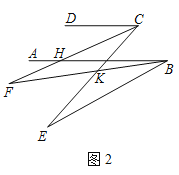
(3)如图3,若P是(2)中的射线BE上一点,G是CD上任一点,PQ∥GN,PQ平分∠BPG,GM平分∠DGP,若∠B=30°,求∠MGN的度数.
相关试题

