【题目】如图,在△ABC中,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=5,BM=2,AC=9,则∠ABC与∠C的关系为( )

A.∠ABC=2∠CB.∠ABC=![]() ∠CC.
∠CC.![]() ∠ABC=∠CD.∠ABC=3∠C
∠ABC=∠CD.∠ABC=3∠C
参考答案:
【答案】D
【解析】
延长BM到E,证明△ABF≌△AEM,利用线段长度推出△BCE是等腰三角形,再根据角度转换求出即可.
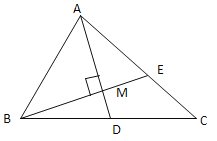
证明:延长BM,交AC于E,
∵AD平分∠BAC,BM⊥AD,
∴∠BAM=∠EAM,∠AMB=∠AME
又∵AM=AM,
∴△ABM≌△AEM,
∴BM=ME,AE=AB,∠AEB=∠ABE,
∴BE=BM+ME=4,AE=AB=5,
∴CE=AC-AE=9-5=4,
∴CE=BE,
∴△BCE是等腰三角形,
∴∠EBC=∠C,
又∵∠ABE=∠AEB=∠C+∠EBC.
∴∠ABE=2∠C,
∴∠ABC=∠ABE+∠EBC=3∠C.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=
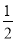 (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).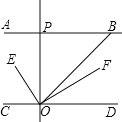
-
科目: 来源: 题型:
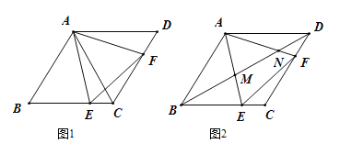
查看答案和解析>>【题目】如图1,已知菱形
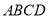 的边长为12,
的边长为12,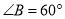 , 点
, 点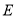 、
、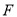 分别是边
分别是边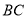 、
、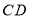 上的动点(不与端点重合),且
上的动点(不与端点重合),且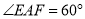 .
.
(1)求证:
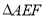 是等边三角形;
是等边三角形;(2)点
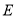 、
、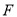 在运动过程中,四边形
在运动过程中,四边形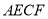 的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;(3)如图2,连接
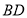 分别与边
分别与边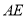 、
、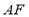 交于
交于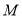 、
、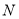 ,当
,当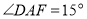 时,求证:
时,求证: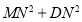
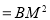 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将△ABC作同样的平移得到△A1B1C1的面积.求:
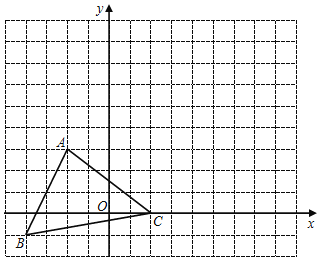
(1)画出△A1B1C1和写出点B1的坐标;
(2)写出平移的过程;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
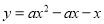 (
( 为非零常数).
为非零常数).(
 )若对称轴是直线
)若对称轴是直线 .
.①求二次函数的解析式.
②二次函数
 (
(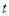 为实数)图象的顶点在
为实数)图象的顶点在 轴上,求
轴上,求 的值.
的值.(
 )把抛物线
)把抛物线 向上平移
向上平移 个单位得到新的抛物线
个单位得到新的抛物线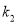 ,若
,若 ,求
,求 的图像落在
的图像落在 轴上方的部分对应的
轴上方的部分对应的 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
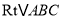 中,
中, 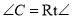 ,
, 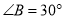 .
.(
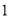 )把
)把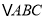 绕点
绕点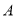 按顺时针方向旋转,得
按顺时针方向旋转,得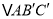 ,
, 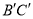 交
交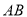 于点
于点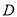 .
.①若
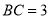 ,旋转角为
,旋转角为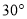 ,求
,求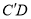 的长.
的长.②若点
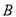 经过的路径与
经过的路径与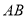 ,
, 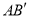 所围图形的面积与
所围图形的面积与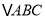 面积的比值是
面积的比值是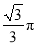 ,求
,求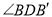 的度数.
的度数.(
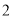 )点
)点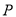 在边
在边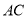 上,
上, 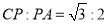 ,把
,把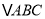 绕着点
绕着点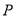 逆时针旋转
逆时针旋转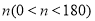 度后,如果点
度后,如果点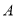 恰好落在初始
恰好落在初始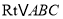 的边上,求
的边上,求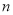 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
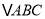 中,
中, 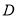 为
为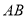 边上一点,过点
边上一点,过点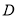 作
作 交
交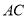 于点
于点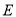 ,以
,以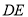 为折线,将
为折线,将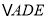 翻折,设所得的
翻折,设所得的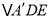 与梯形
与梯形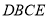 重叠部分的面积为
重叠部分的面积为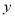 .
.(
 )如图(甲),若
)如图(甲),若 ,
, 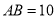 ,
,  ,
, 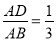 ,则
,则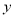 的值为__________.
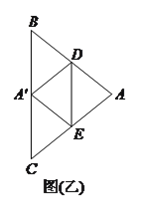
的值为__________.(
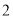 )如图(乙),若
)如图(乙),若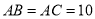 ,
, 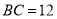 ,
, 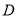 为
为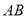 中点,则
中点,则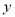 的值为__________.
的值为__________.(
 )若
)若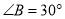 ,
, 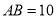 ,
, 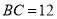 ,设
,设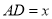 .
.①求
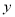 与
与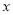 的函数解析式.
的函数解析式.②
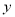 是否有最大值,若有,求出
是否有最大值,若有,求出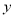 的最大值;若没有,请说明理由.
的最大值;若没有,请说明理由.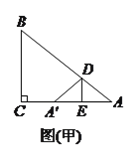
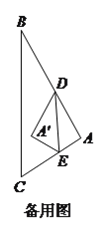
相关试题

