【题目】目前使用节能灯照明已经基本普及,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、售价如表:
进价(元/只) | 售价(元/只) | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
(1)若商场某一天销售节能灯中,销售甲型的只数是乙型的只数的3倍,销售所收的款是9000元,问这天销售节能灯为多少只?
(2)若商场购进节能灯的货款为38000元时,商场销售完节能灯所得利润为多少元?
参考答案:
【答案】(1)这天销售节能灯为240只;(2)商场销售完节能灯所得利润为10000元.
【解析】
(1)根据题意和表格中的数据可以列出相应的方程,从而可以得到这天销售节能灯为多少只;
(2)根据题意和表格中的数据可以列出相应的方程,从而可以得到商场购进甲种和乙种节能灯的只数,然后再根据表格中的数据即可得到商场销售完节能灯所得利润为多少元.
(1)设这天销售的乙型的节能灯为![]() 只,则甲型节能灯为
只,则甲型节能灯为![]() 只
只
![]()
解得,![]()
则![]()
![]() (只)
(只)
答:这天销售节能灯为![]() 只.
只.
(2)设商场购进甲种节能灯为![]() 只,则乙种节能灯为
只,则乙种节能灯为![]() 只
只
![]()
解得,![]()
则![]()
利润为:![]() (元)
(元)
答:商场销售完节能灯所得利润为![]() 元.
元.
-
科目: 来源: 题型:
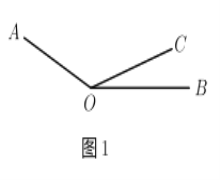
查看答案和解析>>【题目】如图
 ,已知
,已知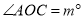 ,
,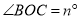 且
且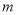 、
、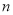 满足等式
满足等式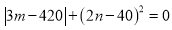 ,射线
,射线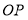 从
从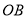 处绕点
处绕点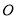 以
以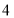 度秒的速度逆时针旋转.
度秒的速度逆时针旋转.(1)试求∠AOB的度数.
(2)如图
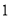 ,当射线
,当射线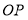 从
从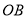 处绕点
处绕点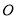 开始逆时针旋转,同时射线
开始逆时针旋转,同时射线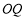 从
从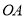 处以
处以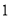 度/秒的速度绕点
度/秒的速度绕点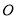 顺时针旋转,当他们旋转多少秒时,使得
顺时针旋转,当他们旋转多少秒时,使得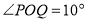 ?
?
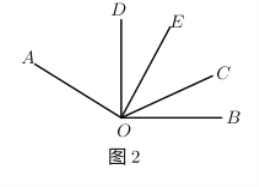
(3)如图
 ,若射线
,若射线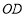 为
为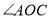 的平分线,当射线
的平分线,当射线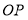 从
从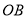 处绕点
处绕点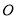 开始逆时针旋转,同时射线
开始逆时针旋转,同时射线 从射线
从射线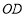 处以
处以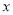 度秒的速度绕点
度秒的速度绕点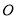 顺时针旋转,使得这两条射线重合于射线
顺时针旋转,使得这两条射线重合于射线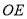 处(
处(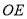 在
在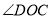 的内部)时,且
的内部)时,且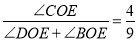 ,试求
,试求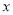 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上点A、B、C所表示的数分别是﹣2、+8、x,AC=6.
(1)画出数轴并标出点A、B的位置.
(2)确定x的值为 .
(3)若点M,N分别是AB,AC的中点,求线段MN的长度.
-
科目: 来源: 题型:
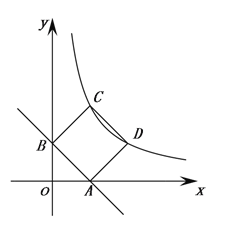
查看答案和解析>>【题目】如图:一次函数y=kx+b的图像交x轴正半轴于点A、y轴正半轴于点B,且OA=OB=1.以线段AB为边在第一象限作正方形ABCD,点D在反比例函数y=
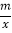 图像上.
图像上.(1)求一次函数的关系式,并判断点C是否在反比例函数y=
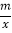 图像上;
图像上;(2)在直线AB上找一点P,使PC+PD的值最小,并求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:
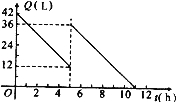
(1)机动车行驶 h后加油;
(2)加油前油箱余油量Q与行驶时间t的函数关系式是 ;
(3)中途加油 L;
(4)如果加油站距目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
-
科目: 来源: 题型:
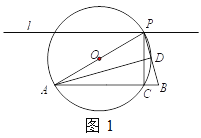
查看答案和解析>>【题目】如图1,已知AB=8,直线l与AB平行,且l与AB的距离为4,P是l上的动点,过点P作PC ⊥AB,垂足为C,点C不与A,B重合,过A,C,P三点作⊙O.
(1)若⊙O与线段PB交于点D,∠PAD=22.5°,则∠APB等于多少度?
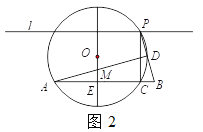
(2)如图2,⊙O与线段PB的一个公共点为D,一条直径垂直AB于点E,且与AD交于点M.
①若ME=
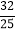 ,求AE的长;
,求AE的长; ②当ME的长度最大时,判断直线PB与⊙O的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=a(x+1)(x-m) (a为常数,a
 1)的图像过点(1,2).
1)的图像过点(1,2).(1)当a=2时,求m的值;
(2)试说明方程a(x+1)(x-m)=0两根之间(不包括两根)存在唯一整数,并求出这个整数;
(3)设M(n,y1)、N(n+1,y2)是抛物线上两点,当n <-1时,试比较y1与y2的大小.
相关试题

