【题目】某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:
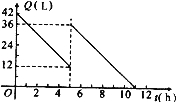
(1)机动车行驶 h后加油;
(2)加油前油箱余油量Q与行驶时间t的函数关系式是 ;
(3)中途加油 L;
(4)如果加油站距目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
参考答案:
【答案】(1)5;(2)Q=42﹣6t(0≤t≤5);(3)24;(4)油箱中的油够用.
【解析】
试题分析:(1)图象上x=5时,对应着两个点,油量一多一少,可知此时加油了;
(2)因为x=0时,Q=42,x=5时,Q=12,所以出发前油箱内余油量42L,行驶5h后余油量为12L,共用去30L,因此每小时耗油量为6L,由此即可写出函数解析式;
(3)因为x=5时,y有两个值12,36,所以加油(36﹣12)L;
(4)因为由图象知,加油后还可行驶6小时,即可行驶40×6千米,然后同230千米做比较,即可求出答案.
试题解析:(1)5;
(2)∵出发前油箱内余油量42L,行驶5h后余油量为12L,共用去30L,
因此每小时耗油量为6L,
∴Q=42﹣6t(0≤t≤5);
(3)36﹣12=24,因此中途加油24L;
(4)由图可知,加油后可行驶6h,
所以加油后行驶40×6=240km,
∵240>230,
∴油箱中的油够用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上点A、B、C所表示的数分别是﹣2、+8、x,AC=6.
(1)画出数轴并标出点A、B的位置.
(2)确定x的值为 .
(3)若点M,N分别是AB,AC的中点,求线段MN的长度.
-
科目: 来源: 题型:
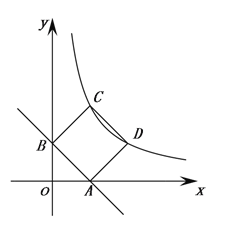
查看答案和解析>>【题目】如图:一次函数y=kx+b的图像交x轴正半轴于点A、y轴正半轴于点B,且OA=OB=1.以线段AB为边在第一象限作正方形ABCD,点D在反比例函数y=
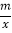 图像上.
图像上.(1)求一次函数的关系式,并判断点C是否在反比例函数y=
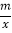 图像上;
图像上;(2)在直线AB上找一点P,使PC+PD的值最小,并求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前使用节能灯照明已经基本普及,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、售价如表:
进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)若商场某一天销售节能灯中,销售甲型的只数是乙型的只数的3倍,销售所收的款是9000元,问这天销售节能灯为多少只?
(2)若商场购进节能灯的货款为38000元时,商场销售完节能灯所得利润为多少元?
-
科目: 来源: 题型:
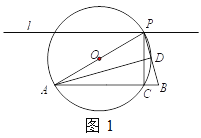
查看答案和解析>>【题目】如图1,已知AB=8,直线l与AB平行,且l与AB的距离为4,P是l上的动点,过点P作PC ⊥AB,垂足为C,点C不与A,B重合,过A,C,P三点作⊙O.
(1)若⊙O与线段PB交于点D,∠PAD=22.5°,则∠APB等于多少度?
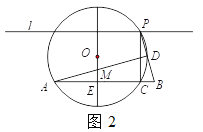
(2)如图2,⊙O与线段PB的一个公共点为D,一条直径垂直AB于点E,且与AD交于点M.
①若ME=
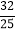 ,求AE的长;
,求AE的长; ②当ME的长度最大时,判断直线PB与⊙O的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=a(x+1)(x-m) (a为常数,a
 1)的图像过点(1,2).
1)的图像过点(1,2).(1)当a=2时,求m的值;
(2)试说明方程a(x+1)(x-m)=0两根之间(不包括两根)存在唯一整数,并求出这个整数;
(3)设M(n,y1)、N(n+1,y2)是抛物线上两点,当n <-1时,试比较y1与y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角△ABC中,AD是BC边上的高.∠BAF=∠CAG=90°,且AB=AF=AC=AG.连接FG,交DA的延长线于点E,连接BG,CF.下列结论:①∠FAG+∠BAC=180°;②BG=CF;③BG⊥CF;④∠EAF=∠ABC.其中一定正确的个数是( )
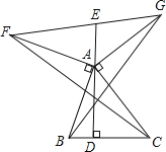
A.4个B.3个C.2个D.1个
相关试题

