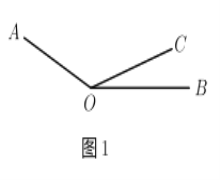
【题目】如图![]() ,已知
,已知![]() ,
,![]() 且
且![]() 、
、![]() 满足等式
满足等式![]() ,射线
,射线![]() 从
从![]() 处绕点
处绕点![]() 以
以![]() 度秒的速度逆时针旋转.
度秒的速度逆时针旋转.
(1)试求∠AOB的度数.
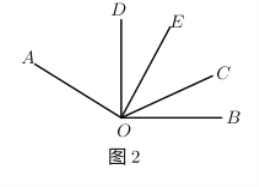
(2)如图![]() ,当射线
,当射线![]() 从
从![]() 处绕点
处绕点![]() 开始逆时针旋转,同时射线
开始逆时针旋转,同时射线![]() 从
从![]() 处以
处以![]() 度/秒的速度绕点
度/秒的速度绕点![]() 顺时针旋转,当他们旋转多少秒时,使得
顺时针旋转,当他们旋转多少秒时,使得![]() ?
?
(3)如图![]() ,若射线
,若射线![]() 为
为![]() 的平分线,当射线
的平分线,当射线![]() 从
从![]() 处绕点
处绕点![]() 开始逆时针旋转,同时射线
开始逆时针旋转,同时射线![]() 从射线
从射线![]() 处以
处以![]() 度秒的速度绕点
度秒的速度绕点![]() 顺时针旋转,使得这两条射线重合于射线
顺时针旋转,使得这两条射线重合于射线![]() 处(
处(![]() 在
在![]() 的内部)时,且
的内部)时,且![]() ,试求
,试求![]() .
.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)根据非负数的性质求得m=140,n=20,即可得到结果;
(2)设他们旋转x秒时,使得∠POQ=10°,则∠AOQ=x°,∠BOP=4x°.分①当射线OP与射线OQ相遇前,②当射线OP与射线OQ相遇后,两种情况,分别列方程求解即可;
(3)设t秒后这两条射线重合于射线OE处,则∠BOE=4t°,先根据角平分线的定义可得∠COD的度数,即可求得∠BOD的度数,再根据![]() 即可求得∠COE的度数,从而得到∠DOE、∠BOE的度数,求出时间t,再列方程求x即可.
即可求得∠COE的度数,从而得到∠DOE、∠BOE的度数,求出时间t,再列方程求x即可.
解:(1)∵![]() ,
,
∴3m420=0且2n40=0,
∴m=140,n=20,
∴∠AOC=140°,∠BOC=20°,
∴∠AOB=∠AOC+∠BOC=160°;
(2)设他们旋转x秒时,使得∠POQ=10°,则∠AOQ=x°,∠BOP=4x°,
①当射线OP与射线OQ相遇前有:∠AOQ+∠BOP+∠POQ=∠AOB=160°,
即:x+4x+10=160,
解得:x=30;
②当射线OP与射线OQ相遇后有:∠AOQ+∠BOP∠POQ=∠AOB=160°,
即:x+4x10=160,
解得:x=34,
答:当他们旋转30秒或34秒时,使得∠POQ=10°;
(3)设t秒后这两条射线重合于射线OE处,则∠BOE=4t°,
∵OD为∠AOC的平分线,
∴∠COD=![]() ∠AOC=70°,
∠AOC=70°,
∴∠BOD=∠COD+∠BOC=70°+20°=90°,
∵![]() ,
,
∴∠COE=![]() ×90°=40°,则∠DOE=70°-40°=30°,∠BOE=20°+40°=60°,
×90°=40°,则∠DOE=70°-40°=30°,∠BOE=20°+40°=60°,
∴4t=60,
解得:t=15,
∴15x=30,
解得:x=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形
 按如图所示的方式放置,点
按如图所示的方式放置,点 .和.
.和.  分别在直线
分别在直线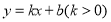 和x轴上,已知点
和x轴上,已知点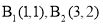 ,则Bn的坐标是____________
,则Bn的坐标是____________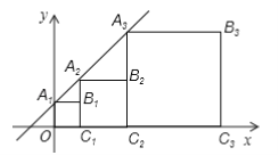
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在A处利用测角仪观测气球C的仰角为30°,然后他沿正对气球方向前进了40m到达B处,此时观测气球的仰角为45°.如果测角仪高度为1m,那么气球的高度是多少?(精确到0.1m)(备注:
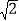 ≈1.414,
≈1.414, ≈1.732)
≈1.732)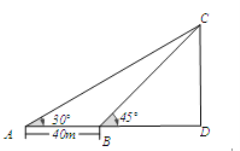
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上点A、B、C所表示的数分别是﹣2、+8、x,AC=6.
(1)画出数轴并标出点A、B的位置.
(2)确定x的值为 .
(3)若点M,N分别是AB,AC的中点,求线段MN的长度.
-
科目: 来源: 题型:
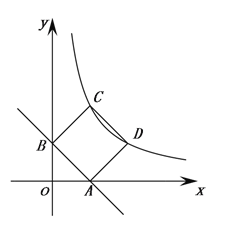
查看答案和解析>>【题目】如图:一次函数y=kx+b的图像交x轴正半轴于点A、y轴正半轴于点B,且OA=OB=1.以线段AB为边在第一象限作正方形ABCD,点D在反比例函数y=
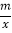 图像上.
图像上.(1)求一次函数的关系式,并判断点C是否在反比例函数y=
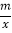 图像上;
图像上;(2)在直线AB上找一点P,使PC+PD的值最小,并求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前使用节能灯照明已经基本普及,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、售价如表:
进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)若商场某一天销售节能灯中,销售甲型的只数是乙型的只数的3倍,销售所收的款是9000元,问这天销售节能灯为多少只?
(2)若商场购进节能灯的货款为38000元时,商场销售完节能灯所得利润为多少元?
相关试题

