【题目】如图,已知四边形ABFC为菱形,点 D、A、E在直线l上,∠BDA=∠BAC=∠CEA.
(1)求证:△ABD≌△CAE;
(2)若∠FBA=60°,连结DF、EF,判断△DEF的形状,并说明理由.

参考答案:
【答案】(1)见解析;(2)△DEF是等边三角形,理由见解析
【解析】(1)利用菱形的性质得出AB=AC,进而得出∠2=∠3,即可利用AAS证明△ABD≌△CAE;
(2)易证△ABF与△ACF均为等边三角形,然后证明△FBD≌△FAE,则DF=EF,∠BFD=∠AFE,从而求得∠DFE的度数,即可证得:△DEF是等边三角形.
(1)证明:∵四边形ABFC为菱形,
∴AB=AC.
∵∠BDA=∠BAC=∠CEA,
又∵![]()
∴∠2=∠3.
在△ABD和△CAE中,
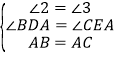
∴△ABD≌△CAE(AAS);
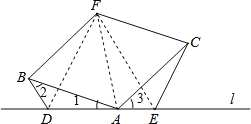
(2)答:△DEF是等边三角形.
连结AF,
∵四边形ABFC为菱形,![]()
∴△ABF与△ACF均为等边三角形,
∴BF=AF,![]()
∵∠2=∠3,
∴∠FBA+∠2=∠FAC+∠3,即∠FBD=∠FAE,
∵△ABD≌△CAE,
∴BD=AE.
在△FBD和△FAE中,
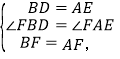
∴△FBD≌△FAE,
∴DF=EF,∠BFD=∠AFE.
∵![]()
∴![]() 即
即![]()
∴△DEF是等边三角形.
-
科目: 来源: 题型:
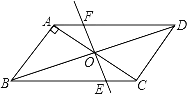
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=
 .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.
-
科目: 来源: 题型:
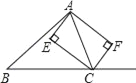
查看答案和解析>>【题目】已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F.
(1)求证:四边形AECF是矩形;
(2)当△ABC满足什么条件时,四边形AECF是正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了完成“舌尖上的中国”的录制,节目组随机抽查了某省“A.奶制品类,B.肉制品类,C.面制品类,D.豆制品类”四类特色美食若干种,将收集的数据整理并绘制成下面两幅尚不完整的统计图,请根据图中信息完成下列问题:
(1)这次抽查了四类特色美食共 种,扇形统计图中a= ,扇形统计图中A部分圆心角的度数为 ;
(2)补全条形统计图;
(3)如果全省共有这四类特色美食120种,请你估计约有多少种属于“豆制品类”?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,四边形ABCD是正方形,∠MAN=45°,它的两边AM、AN分别交CB、DC与点M、N,连结MN,作AH⊥MN,垂足为点H
(1)如图1,猜想AH与AB有什么数量关系?并证明;
(2)如图2,已知∠BAC=45°,AD⊥BC于点D,且BD=2,CD=3,求AD的长;
小萍同学通过观察图①发现,△ABM和△AHM关于AM对称,△AHN和△ADN关于AN对称,于是她巧妙运用这个发现,将图形如图③进行翻折变换,解答了此题.你能根据小萍同学的思路解决这个问题吗?

-
科目: 来源: 题型:
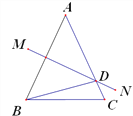
查看答案和解析>>【题目】如图,在△ABC,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初三数学课本上,用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
x
…
﹣2
﹣1
0
1
2
…
y
…
﹣15.5
﹣5
﹣3.5
﹣2
﹣3.5
…
根据表格上的信息回答问题:该二次函数y=ax2+bx+c在x=3时,y= .
相关试题

